在前面的博文中,我们介绍了5种查找算法,本文主要介绍哈希表及哈希查找算法。
在介绍哈希查找算法之前,我们需要详细了解什么是哈希表及其构造实现方法。
哈希表
哈希表的基本思想
我们知道,数组的最大特点就是:寻址容易,插入和删除困难;而链表正好相反,寻址困难,而插入和删除操作容易。那么如果能够结合两者的优点,做出一种寻址、插入和删除操作同样快速容易的数据结构。这就是哈希表创建的基本思想,哈希表就是这样一个集查找、插入和删除操作于一身的数据结构。
哈希表的一些基本概念
哈希表(Hash Table):也叫散列表,是根据关键码值(Key-Value)而直接进行访问的数据结构,也就是我们常用到的map。
哈希函数:也称散列函数,是Hash表的映射函数,它可以把查找表中的关键字映射成该关键字对应的地址函数,表示如下:
$$
Hash(key) = Addr,(地址可以是数组下标、索引、内存地址等)
$$
哈希函数能使对一个数据序列的访问过程变得更加迅速有效,通过哈希函数数据元素能够被很快的进行定位。- 冲突:两个不同的关键字,由于散列函数值相同,因而被映射到同一表位置上。该现象称为冲突(Collision)或碰撞。
- 尽量减少冲突
- 冲突不可避免,要设计好处理冲突的方法
散列函数的构造方法
- 定义域必须包含全部需要存储的关键字
- 地址等概率,均匀的分布在整个地址空间
- 函数尽量简单,较短时间内能算出任一关键字地址
哈希表有很多种不同的实现方法,为了实现哈希表的创建,这些所有的方法都离不开两个问题——“定址”和“解决冲突”
哈希表的定址方法
- 直接定址法:直接取关键字的某个线性函数值作为散列地址,例如:
$$
H(key) = a \times key + b,(a和b均为常数)
$$
适合关键字分布基本连续的情况,否则容易造成存储空间浪费。
- 除留余数法:(最常用) 假定表长为m,取一个不大于m但最接近或者等于m的质数P,例如:
$$
H(key) = key\%P
$$ - 数字分析法:比如有一组$value1=112233,value2=112633,value3=119033$,针对这样的数我们分析数中间两个数比较波动,其他数不变。那么我们取key的值就可以是$key1=22,key2=26,key3=90$。
适合于已知关键字的集合分布,关键字位数较大的情况。
- 平方取中法:取关键字的平法值的中间几位作为散列地址。
适合于不是道关键字分布,且关键字每一位取值不均匀或均小于散列地址所需的位数。
- 折叠法:举个例子,比如$value=135790$,要求key是2位数的散列值。那么我们将$value$变为$13+57+90=160$,然后去掉高位$“1”$,此时$key=60$,这就是他们的哈希关系。这样做的目的就是key与每一位value都相关,来达到“散列地址”尽可能分散的目的。
适合于不需要知道关键字分布,关键字位数较多的情况。
哈希表解决冲突的方法
- 开放定址法:
如果两个数据元素的哈希值相同,则在哈希表中为后插入的数据元素另外选择一个表项。当程序查找哈希表时,如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素,程序就会继续往后查找,直到找到一个符合查找要求的数据元素,或者遇到一个空的表项。
假设已经选定散列函数为$H(key)$,下面用$H_i$表示发生冲突后第$i$次探测的散列地址。
$$
H_{i} = (H(key)+d_{i})\%m
$$
其中,$i=1, 2, …,k (k<=1)$;$m$表示散列长度,$d_i$表示增量序列。
增量序列$d_i$通常有4种取法:
- 线性探测法:$d_i=1,2,…, m-1$,可能造成大量元素在相邻地址聚集,降低查找效率。
- 平方探测法:$d_i=1^2,-1^2,2^2,-2^2,…,-k^2,(k<=m/2)$,m必须是一个可表示为$4k+3$的质数。避免出现“堆积问题”,但是不能探测全部单元(至少一半)。
- 再散列法:$d_i=Hash_{2}(key)$,使用2个散列函数。
- 伪随机序列法:$d_i=$伪随机序列
注意:开放定址情形下,不能随便物理删除表中已有的元素,这样会截断其他具有相同散列地址元素查找地址;应做删除标记,逻辑删除。
以线性探测为例(定址法选择取余法),举例如下:
散列过程如下图所示:
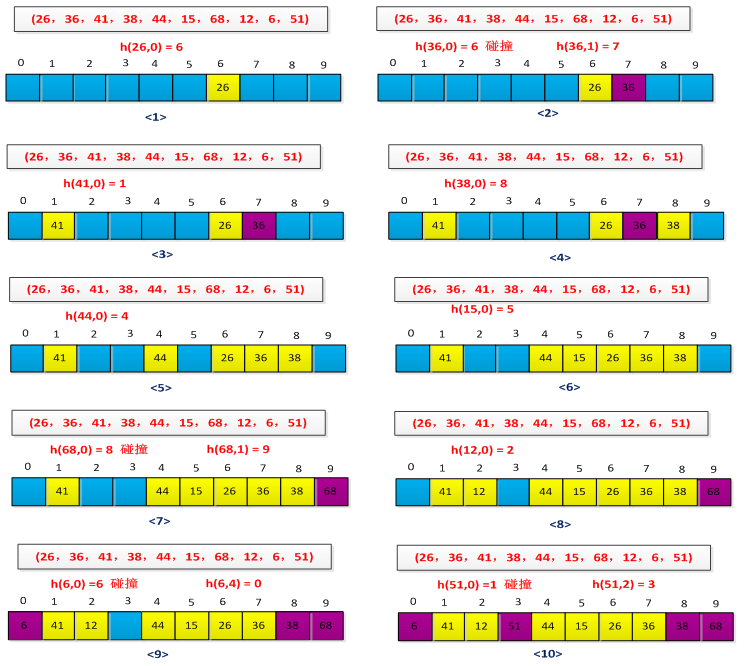
我们可以发现,冲突次数还是比较多的,这是因为P的取值没选好,前面讲过:假定表长为m,取一个不大于m但最接近或者等于m的质数P,这里表长m=10,P最好取7,而图中取了10。
- 拉链法:
将哈希值相同的数据元素存放在一个链表中,在查找哈希表的过程中,当查找到这个链表时,必须采用线性查找方法。适用于经常进行插入、删除的情况。
定址法选择取余法,举例如下:
设有一组关键字为(26,36,41,38,44,15,68,12,6,51),初始情况如下图所示:
最终结果如下图所示:
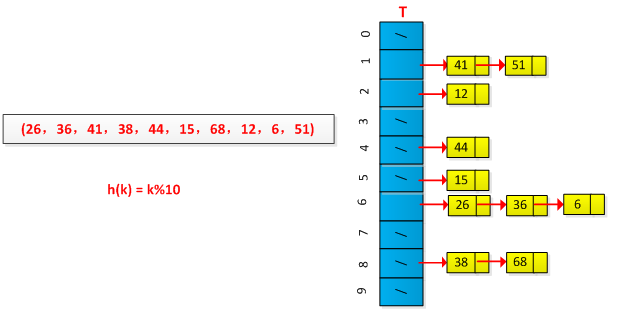
散列查找及性能分析
查找过程与构造过程基本一致
查找效率三因素:散列函数、处理冲突的方法、哈希表装填因子$(\alpha)$
$$
\alpha = \frac{表中记录数}{散列表长度} = \frac{n}{m}
$$
平均查找长度依赖于$\alpha$,$\alpha$越大,记录越“满”,发生冲突的可能性越大。
下面贴一张哈希表中查找失败和成功时,平均查找程度的计算例子

拓展:如果关键字是字符串怎么办? (详见参考资料)
- 将字符串的所有的字符的ASCII码值进行相加,将所得和作为元素的关键字
- 假设关键字至少有三个字母构成,散列函数只是取前三个字母进行散列
- 借助Horner’s 规则,构造一个质数(通常是37)的多项式,(非常的巧妙,不知道为何是37)。计算公式为:$key[keysize-i-1]*37^i, 0<=i<keysize$求和。
哈希查找
介绍完如何构造哈希表后,我们来看一下哈希查找算法。
算法简介
哈希表就是一种以键-值(key-indexed) 存储数据的结构,只要输入待查找的值即key,即可查找到其对应的索引值(地址)。
算法思想
哈希的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键。
算法流程
- 用给定的哈希函数构造哈希表;
- 根据选择的冲突处理方法解决地址冲突;
- 在哈希表的基础上执行哈希查找。
哈希表(空间换时间)是一个在时间和空间上做出权衡的经典例子。如果没有内存限制,那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1);如果没有时间限制,那么我们可以使用无序数组并进行顺序查找,这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。
复杂度分析:单纯论查找复杂度:对于无冲突的Hash表而言,查找复杂度为O(1)(注意,在查找之前我们需要构建相应的Hash表)。
算法实现
这边找了一个除留余数法加线性开放定址法的代码实例,来源于c实现哈希查找
1 | //采用除数取留法确定地址,利用线性开放地址法处理冲突问题,2016.5.28 |
