二叉树的遍历
所谓二叉树的遍历,是指按某条搜索路径访问树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
由二叉树的递归定义可知,遍历一棵二叉树便要决定对根结点$N$、左子树$L$和右子树$R$的访问顺序。按照先遍历左子树再遍历右子树的原则,常见的遍历次序有:
- 前序遍历:(N L R)
- 中序遍历:(L N R)
- 后序遍历:(L R L)
这里的序指的是根结点何时被访问

在介绍3种遍历算法前,我们先给出二叉树的存储结构和建立二叉树的代码:
所有代码均来自c实现树(二叉树)的建立和遍历算法(一)(前序,中序,后序)
二叉树的存储结构(二叉链表)
1
2
3
4
5
6//二叉树的二叉链表结构,也就是二叉树的存储结构,1个数据域,2个指针域(分别指向左右孩子)
typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;建立二叉树(此处以前序遍历的方式建立)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17//二叉树的建立,按前序遍历的方式建立二叉树,当然也可以以中序或后序的方式建立二叉树
void CreateBiTree(BiTree *T)
{
ElemType ch;
cin >> ch;
if (ch == '#')
*T = NULL; //保证是叶结点
else
{
*T = (BiTree)malloc(sizeof(BiTNode));
//if (!*T)
//exit(OVERFLOW); //内存分配失败则退出。
(*T)->data = ch;//生成结点
CreateBiTree(&(*T)->lchild);//构造左子树
CreateBiTree(&(*T)->rchild);//构造右子树
}
}
下面给出2种算法,分别实现三种遍历方式
递归算法
程序实现
1 | /递归方式前序遍历二叉树 |
下面是完整的实现代码
1 |
|
注意:
- 建立二叉树时,这里是以前序遍历的方式,输入的是扩展二叉树,也就是要告诉计算机什么是叶结点,否则将一直递归,当输入“#”时,指针指向NULL,说明是叶结点。
如下图为扩展二叉树:(前序遍历为:ABDG##H###CE#I##F##)
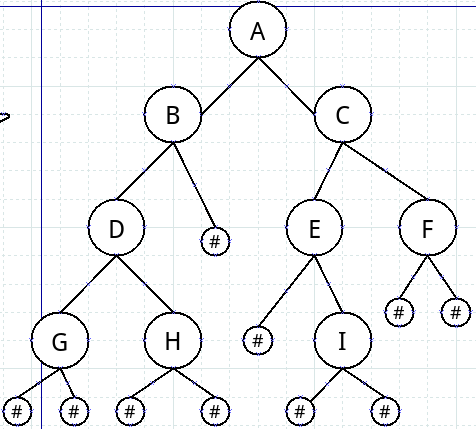
operation1( )函数只是对各个结点的输出;operation2( )函数不仅输出了各个结点,同时输出了结点所在的层数。
运行结果
- 只是运行了
operation2( )函数,有层数输出:
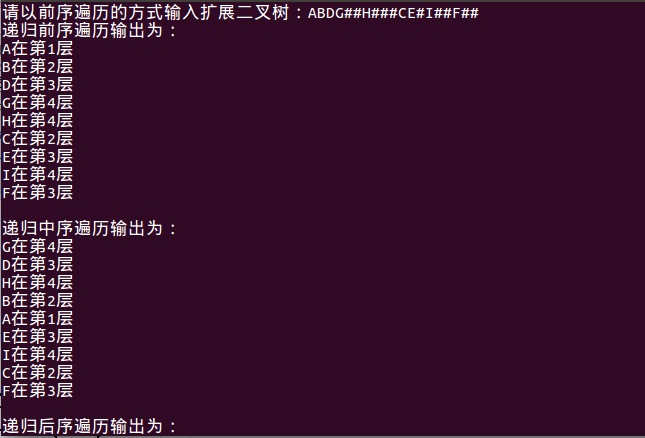
- 只是运行了
operation1( )函数,输出值:

非递归算法
- 我们可以借助栈,实现3种遍历的非递归算法
- 除此之外,还给出了二叉树的层次遍历算法,所谓层次遍历,就是自顶向下、自左至右的遍历二叉树中的元素,可以借助队列实现。
程序实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128//非递归方式前序遍历
/* 思路:将T入栈,遍历左子树;遍历完左子树返回时,栈顶元素应为T,出栈,再先序遍历T的右子树。*/
void PreOrder(BiTree T){
stack<BiTree> stack;
//p是遍历指针
BiTree p = T;
//p不为空或者栈不空时循环
while (p || !stack.empty())
{
if (p != NULL)
{
//存入栈中
stack.push(p);
//对树中的结点进行操作
operation1(p->data);
//遍历左子树
p = p->lchild;
}
else
{
//退栈
p = stack.top();
stack.pop();
//访问右子树
p = p->rchild;
}
}
}
//非递归中序遍历
void InOrder(BiTree T)
{
stack<BiTree> stack;
//p是遍历指针
BiTree p = T;
//p不为空或者栈不空时循环
while (p || !stack.empty())
{
if (p != NULL)
{
//存入栈中
stack.push(p);
//遍历左子树
p = p->lchild;
}
else
{
//退栈
p = stack.top();
operation1(p->data); //对树中的结点进行操作
stack.pop();
//访问右子树
p = p->rchild;
}
}
}
//非递归后序遍历
typedef struct BiTNodePost{
BiTree biTree;
char tag;
}BiTNodePost, *BiTreePost;
void PostOrder(BiTree T)
{
stack<BiTreePost> stack;
//p是遍历指针
BiTree p = T;
BiTreePost BT;
//栈不空或者p不空时循环
while (p != NULL || !stack.empty())
{
//遍历左子树
while (p != NULL)
{
BT = (BiTreePost)malloc(sizeof(BiTNodePost));
BT->biTree = p;
//访问过左子树
BT->tag = 'L';
stack.push(BT);
p = p->lchild;
}
//左右子树访问完毕访问根节点
while (!stack.empty() && (stack.top())->tag == 'R')
{
BT = stack.top();
//退栈
stack.pop();
p=BT->biTree;
cout<<BT->biTree->data<<" ";
}
//遍历右子树
if (!stack.empty())
{
BT = stack.top();
//访问过右子树
BT->tag = 'R';
p = BT->biTree;
p = p->rchild;
}
}
}
//层次遍历
void LevelOrder(BiTree T)
{
BiTree p = T;
queue<BiTree> queue;
//根节点入队
queue.push(p);
//队列不空循环
while (!queue.empty())
{
//对头元素出队
p = queue.front();
//访问p指向的结点
operation1(p->data);
//退出队列
queue.pop();
//左孩子不为空,将左孩子入队
if (p->lchild != NULL)
{
queue.push(p->lchild);
}
//右孩子不空,将右孩子入队
if (p->rchild != NULL)
{
queue.push(p->rchild);
}
}
}
下面是完整的实现代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
using namespace std;
typedef char ElemType;
//二叉树的二叉链表结构,也就是二叉树的存储结构,1个数据域,2个指针域(分别指向左右孩子)
typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
//二叉树的建立,按前序遍历的方式建立二叉树,当然也可以以中序或后序的方式建立二叉树
void CreateBiTree(BiTree *T)
{
ElemType ch;
cin >> ch;
if (ch == '#')
*T = NULL; //保证是叶结点
else
{
*T = (BiTree)malloc(sizeof(BiTNode));
//if (!*T)
//exit(OVERFLOW); //内存分配失败则退出。
(*T)->data = ch;//生成结点
CreateBiTree(&(*T)->lchild);//构造左子树
CreateBiTree(&(*T)->rchild);//构造右子树
}
}
//表示对遍历到的结点数据进行的处理操作,此处操作是将树结点前序遍历输出
void operation1(ElemType ch)
{
cout << ch << " ";
}
//此处在输出的基础上,并输出层数
void operation2(ElemType ch, int level)
{
cout << ch << "在第" << level << "层" << " ";
}
//递归方式前序遍历二叉树
void PreOrderTraverse(BiTree T, int level)
{
if (T == NULL)
return;
/*此处表示对遍历的树结点进行的操作,根据你自己的要求进行操作,这里只是输出了结点的数据*/
operation1(T->data);
//operation2(T->data, level); //输出了层数
PreOrderTraverse(T->lchild, level + 1);
PreOrderTraverse(T->rchild, level + 1);
}
//递归方式中序遍历二叉树
void InOrderTraverse(BiTree T,int level)
{
if(T==NULL)
return;
InOrderTraverse(T->lchild,level+1);
operation1(T->data);
//operation2(T->data, level); //输出了层数
InOrderTraverse(T->rchild,level+1);
}
//递归方式后序遍历二叉树
void PostOrderTraverse(BiTree T,int level)
{
if(T==NULL)
return;
PostOrderTraverse(T->lchild,level+1);
PostOrderTraverse(T->rchild,level+1);
operation1(T->data);
//operation2(T->data, level); //输出了层数
}
//非递归方式前序遍历
/* 思路:将T入栈,遍历左子树;遍历完左子树返回时,栈顶元素应为T,出栈,再先序遍历T的右子树。*/
void PreOrder(BiTree T){
stack<BiTree> stack;
//p是遍历指针
BiTree p = T;
//p不为空或者栈不空时循环
while (p || !stack.empty())
{
if (p != NULL)
{
//存入栈中
stack.push(p);
//对树中的结点进行操作
operation1(p->data);
//遍历左子树
p = p->lchild;
}
else
{
//退栈
p = stack.top();
stack.pop();
//访问右子树
p = p->rchild;
}
}
}
//非递归中序遍历
void InOrder(BiTree T)
{
stack<BiTree> stack;
//p是遍历指针
BiTree p = T;
//p不为空或者栈不空时循环
while (p || !stack.empty())
{
if (p != NULL)
{
//存入栈中
stack.push(p);
//遍历左子树
p = p->lchild;
}
else
{
//退栈
p = stack.top();
operation1(p->data); //对树中的结点进行操作
stack.pop();
//访问右子树
p = p->rchild;
}
}
}
//非递归后序遍历
typedef struct BiTNodePost{
BiTree biTree;
char tag;
}BiTNodePost, *BiTreePost;
void PostOrder(BiTree T)
{
stack<BiTreePost> stack;
//p是遍历指针
BiTree p = T;
BiTreePost BT;
//栈不空或者p不空时循环
while (p != NULL || !stack.empty())
{
//遍历左子树
while (p != NULL)
{
BT = (BiTreePost)malloc(sizeof(BiTNodePost));
BT->biTree = p;
//访问过左子树
BT->tag = 'L';
stack.push(BT);
p = p->lchild;
}
//左右子树访问完毕访问根节点
while (!stack.empty() && (stack.top())->tag == 'R')
{
BT = stack.top();
//退栈
stack.pop();
p=BT->biTree;
cout<<BT->biTree->data<<" ";
}
//遍历右子树
if (!stack.empty())
{
BT = stack.top();
//访问过右子树
BT->tag = 'R';
p = BT->biTree;
p = p->rchild;
}
}
}
//层次遍历
void LevelOrder(BiTree T)
{
BiTree p = T;
queue<BiTree> queue;
//根节点入队
queue.push(p);
//队列不空循环
while (!queue.empty())
{
//对头元素出队
p = queue.front();
//访问p指向的结点
operation1(p->data);
//退出队列
queue.pop();
//左孩子不为空,将左孩子入队
if (p->lchild != NULL)
{
queue.push(p->lchild);
}
//右孩子不空,将右孩子入队
if (p->rchild != NULL)
{
queue.push(p->rchild);
}
}
}
int main()
{
int level = 1; //表层数
BiTree T = NULL;
cout << "请以前序遍历的方式输入扩展二叉树:"; //类似输入AB#D##C##
CreateBiTree(&T);// 建立二叉树,没有树,怎么遍历
cout << "递归前序遍历输出为:" << endl;
PreOrderTraverse(T, level);//进行前序遍历,其中operation1()和operation2()函数表示对遍历的结点数据进行的处理操作
cout << endl;
cout << "递归中序遍历输出为:" << endl;
InOrderTraverse(T, level);
cout << endl;
cout << "递归后序遍历输出为:" << endl;
PostOrderTraverse(T, level);
cout << endl;
cout<<"非递归前序遍历输出为:"<<endl;
PreOrder(T);
cout<<endl;
cout<<"非递归前序遍历输出为:"<<endl;
InOrder(T);
cout<<endl;
cout<<"非递归前序遍历输出为:"<<endl;
PostOrder(T);
cout<<endl;
cout<<"层序遍历输出为:"<<endl;
LevelOrder(T);
cout<<endl;
return 0;
}
运行结果
只是运行了operation1( )函数,输出值:
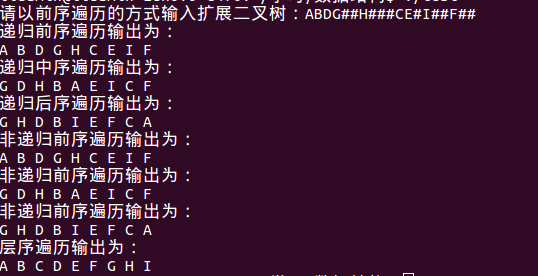
补充:另外一种实现二叉树后序遍历的非递归算法。
1 | void PostOrder(BiTree T){ |
重要结论:
- 二叉树的前序和中序序列能唯一确定一棵二叉树
- 二叉树的后序和中序序列能唯一确定一棵二叉树
- 二叉树的层次和中序序列能唯一确定一棵二叉树
