本文主要介绍线索二叉树和树、二叉树、森林三者之间的相互转换。
对于线索二叉树,这里只做简单介绍,着重还是要理解上篇博文中二叉树的各种遍历算法。
线索二叉树
基本概念
遍历二叉树的实质就是对一个非线性结构进行线性化操作,使在这个访问序列中每一个结点(除第一个和最后一个)都有一个直接前驱和直接后继。
传统的链式存储仅能体现一种父子关系,不能直接得到结点在遍历中的前驱和后继。通过观察,我们发现在二叉链表表示的二叉树中存在大量的空指针,若利用这些空链域存放指向其直接前驱或后继的指针,则可以方便的运用某些二叉树操作算法。引入线索二叉树的目的是为了加快查找结点前驱和后继的速度。
在二叉树线索化时,通常规定:
- 若无左子树,令$lchild$指向其前驱结点,若无右子树,令$rchild$指向其后继结点
- 还需增加两个标志域表明当前指针域所指的对象是指向左(右)子结点还是直接前驱(后继)

线索二叉树存储结构描述如下:1
2
3
4
5typedef struct ThreadNode{
ElemType data; //数据元素
struct ThreadNode *lchild,*rchild; //左、右孩子指针
int ltag,rtag; //左、右线索标志
}ThreadNode,*ThreadTree;
线索二叉树的构造
对二叉树的线索化,实质上就是遍历一次二叉树,只是在遍历的过程中,检查当前结点左、右指针域是否为空,若为空,将它们改为指向前驱结点或后继结点的线索。
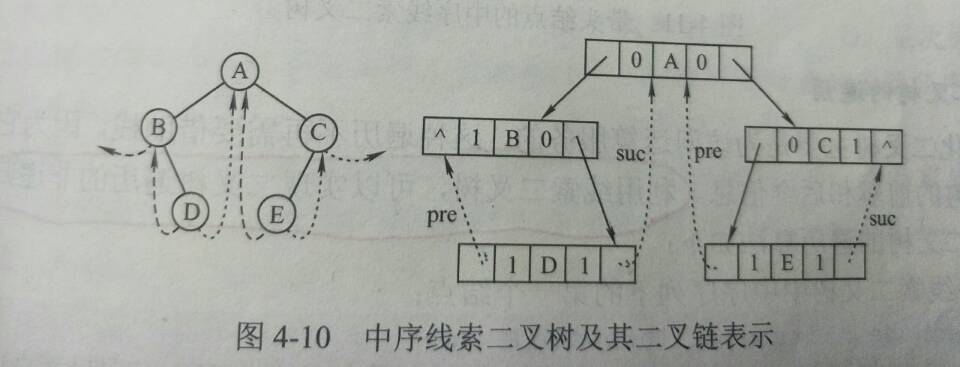
下面以中序线索二叉树建立为例,指针$pre(suc)$指向中序遍历时上一个刚访问过(下一个访问)的结点,如下图所示(中序遍历为 B D A E C):
下面给出中序遍历时对二叉树线索化的递归算法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15void InThread(ThreadTree &p,ThreadTree &pre){
if(p!=NULL){
InThread(p->lchild,pre); //递归,线索化左子树
if(p->lchild==NULL){ //左子树为空,建立前驱线索
p->lchild=pre;
p->tag=1;
}
if(pre!=NULL&&pre->rchild==NULL){
pre->rchild=p; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=p; //标记当前结点成为刚刚访问过的结点
InThread(p->rchild,pre) //递归,线索化右子树
}
}
调用上述方法,建立中序线索二叉树的主过程1
2
3
4
5
6
7
8void CreateInThread(ThreadTree T){
ThreadTree pre=NULL;
if(T!=NULL){ //非空二叉树,线索化
InThread(T,pre); //线索化二叉树
pre->rchild=NULL; //处理遍历的最后一个结点
pre->rtag=1;
}
}
树、森林、二叉树的相互转换
在介绍转换方法前,我们先来看一下树的存储结构

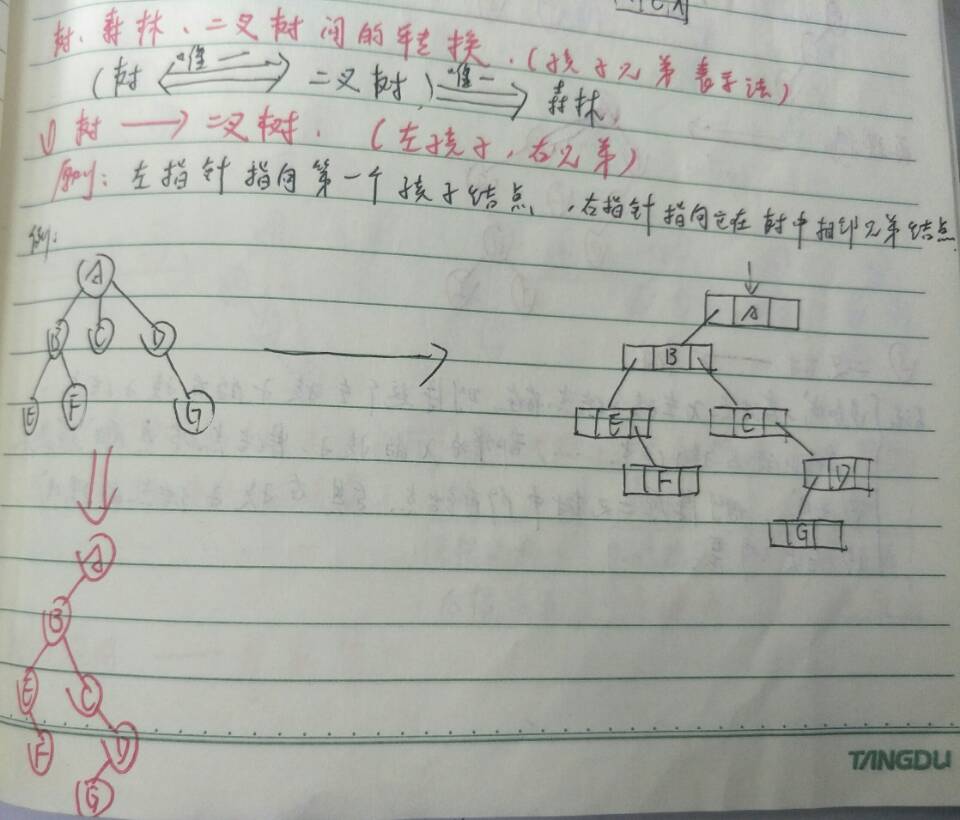
树 —–> 二叉树
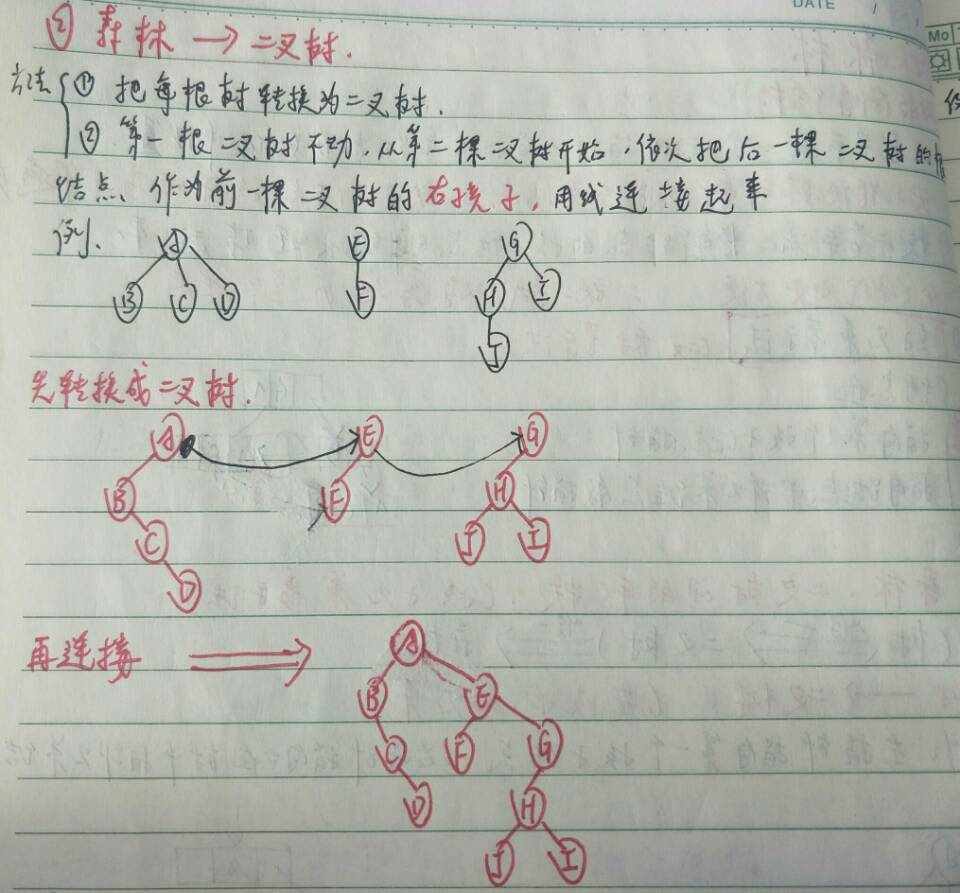
森林 —–> 二叉树
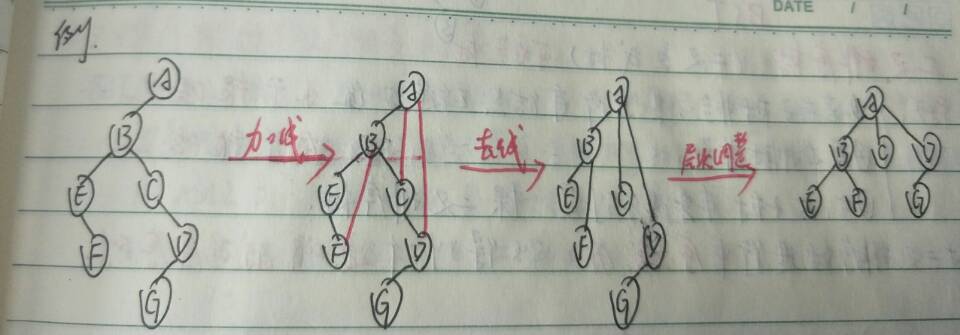
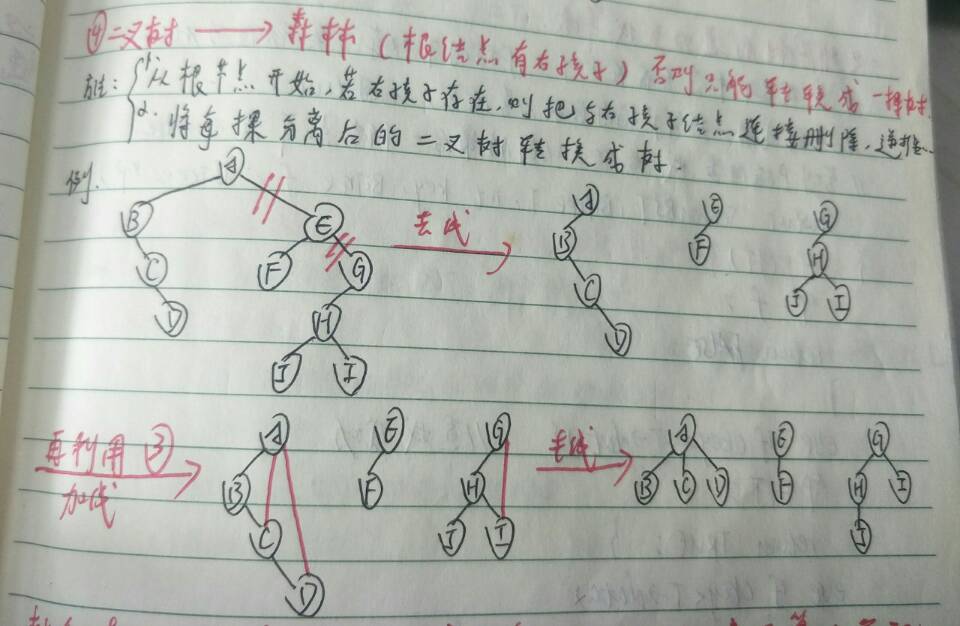
二叉树 —–> 树

二叉树 —–> 森林
树和森林的遍历可采用对应二叉树遍历算法实现,与二叉树遍历的对应关系如下表所示:
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先根遍历 | 先序遍历 | 先序遍历 |
| 后根遍历 | 中序遍历 | 中序遍历 |
