在上篇博文中,我们了解了栈的节本原理和操作。本文主要介绍另外一种操作受限的线性表,队列(Queue)。
队列(Queue)也是一种操作受限的线性表,它只允许在表的一端进行插入,而在另外一端进行删除,满足先进先出(FIFO)。
队列的基本操作
InitQueue(&Q):初始化QueueEmpty(Q):判断队列是否为空EnQueue(&Q,x):入队,若Q未满,将x加入,使之成为新的队尾DeQueue(&Q,&x):出队,若Q非空,删除队头元素,并用x返回GetHead(Q,&x):读队头元素,若Q非空,将队头元素赋值给x
队列的顺序存储结构
分配一块连续的存储单元存放队列中的元素,并附设两个指针front和rear分别指向队头元素和队尾元素的位置。设队头指针指向队头元素,队尾指针指向队尾的下一个位置。
队列的顺序存储类型可描述如下:1
2
3
4
5
typedef struct{
ElemType data[MaxSize]; //存放队列元素
int front,rear; //队头指针和队尾指针
}SqQueue;
初始状态(队空条件)$Q.front==Q.rear==0$
进队操作:队不满时,先送值到队尾元素,再将队尾指针加1
出队操作:队不空时,先取队头元素,再将队头指针加1
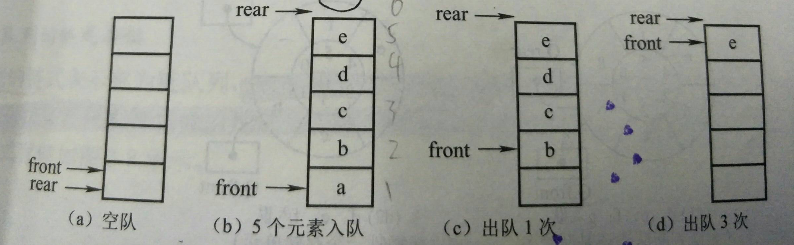
如上图所示,我们可以用$Q.front==Q.rear==0$来判断队列是否为空,但是我们不能用$Q.rear==MaxSize$作队满的条件,如上图(d)所示。
循环队列
为了克服顺序队列的缺点,引出了循环队列,将顺序队列臆造为一个环状空间。

出队入队时,指针按顺时针方向进1,如下图所示:
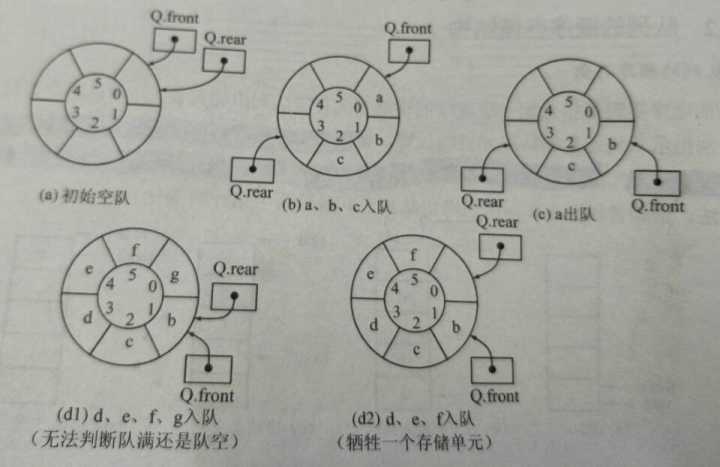
为了区分$Q.front==Q.rear$为队空还是队满,有三种处理方式:
入队时,少用一个队列单元,队头指针在队尾指针的下一个位置时队满
队满条件:$(Q.rear+1)$%$MaxSize==Q.front$
队空条件:$Q.front==Q.rear$
队列中元素个数:$(Q.rear-Q.front+MaxSize)$%$MaxSize$增设表示元素个数的数据成员
队空:$Q.size==0$
队满:$Q.size==MaxSize$增设tag成员,区分队满还是队空(tag表示下一个存储空间是否为空)
tag=0,出队:因为删除导致$Q.front==Q.rear$ (队空)
tag=1,进队:因为插入导致$Q.front==Q.rear$ (队满)
循环队列的基本操作如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28//初始化
void InitQueue(&Q){
Q.rear=Q.front=0;
}
//判断队列是否为空
bool isEmpty(Q){
if(Q.rear==Q.front)
return true;
else
return false;
}
//入队
bool EnQueue(SqQueue &Q,ElemType x){
if((Q.rear+1)%MaxSize==Q.front)
return false;
else
Q.data[Q.rear]=x;
Q.rear=(Q.rear+1)%MaxSize;
return true;
}
//出队
bool DeQueue(SqQueue &Q,ElemType &x){
if(Q,rear==Q.front)
return false;
x=Q.data[Q.front];
Q.front=(Q.front+1)%MaxSize;
return true;
}
队列的链式存储结构
本质上是一个同时带有队头指针和队尾指针的单链表。头指针指向队头结点,尾指针指向队尾结点。
队列的链式存储类型可以描述如下:1
2
3
4
5
6
7typedef struct{
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{
LinkNode *front,*rear;
}LinkQueue;
$Q.front==NULL$且$Q.rear==NULL$,链式队列为空
出队:首先判空,若队列不为空,取出队头元素,删除,让$Q.front$指向下一个结点
进队:建立新结点,将该结点插入链表尾部,并让$Q.rear$指向这个新插入的结点
通常将链式队列设计成一个带头结点的单链表,这样可以统一插入和删除操作。
链式队列的基本操作1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32//初始化
void InitQueue(LinkQueue &Q){
Q.front=Q.rear=(LinkNode *) malloc (sizeof(LinkNode));
Q.front->next=NULL;
}
//判断队列是否为空
bool IsEmpty(LinkQueue Q){
if(Q.front==Q.rear)
return true;
else
return false;
}
//入队
void EnQueue(LinkQueue &Q,ElemType x){
s=(LinkNode *) malloc (sizeof(LinkNode));
s->data=x;
s->next=NULL;
Q.rear->next=s;
Q.rear=s;
}
//出队
bool DeQueue(LinkQueue &Q,ElemType &x){
if(Q.front==Q.rear)
return false;
p=Q.front->next;
x=p->next;
Q.front->next=p->next;
if(Q.rear==p)
Q.rear=Q.front;
free(p);
return true;
}
双端队列
双端队列是指允许两端都可以进行入队和出队操作的队列。

进队:前端进的元素在后端进的元素前面
出队:无论前端还是后端出队,先出的元素排在后出的元素前面
输出受限:允许一端进行插入和删除,另外一端只能插入
输入受限:允许一端进行插入和删除,另外一端只能删除
栈和队列的应用:(以后会详细讲解)
- 栈:括号匹配、表达式求值、递归、进制转换、迷宫求解…
- 队列:二叉树的层次遍历、缓冲区、页面替换算法、广度优先搜索图
特殊矩阵的压缩存储
数组与线性表的关系:数组是线性表的推广。一维数组可以看做是一个线性表,二维数组可以看做元素是线性表的线性表。数组只有存取元素和修改元素操作。
数组的存储结构
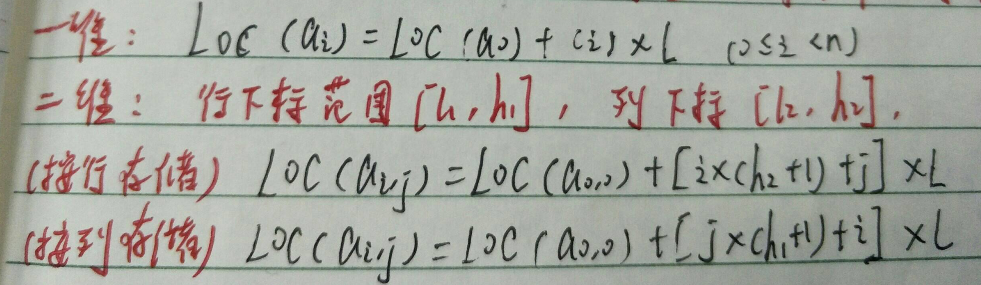
矩阵的压缩存储

