C语言实现七大查找算法（一）

发表于 | 更新于 | 分类于 | 阅读次数
字数统计 3.6k | 阅读时长 14

本文主要介绍数据结构中的查找算法，主要介绍顺序查找、折半查找（二分查找）、树表查找、分块查找、哈希查找（散列）。其他的一些查找算法也会有所介绍。

查找（Searching）就是根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素。

  1. 查找表（Search Table）：由同一类型的数据元素构成的集合
  2. 关键字（Key）：数据元素中某个数据项的值，又称为键值
  3. 主键（Primary Key）：可唯一的标识某个数据元素或记录的关键字

查找表按照操作方式可分为：

  1. 静态查找表（Static Search Table）：只做查找操作的查找表。它的主要操作是：

    • 查询某个“特定的”数据元素是否在表中
    • 检索某个“特定的”数据元素和各种属性

  2. 动态查找表（Dynamic Search Table）：在查找中同时进行插入或删除等操作：

    • 查找时插入数据
    • 查找时删除数据

平均查找长度（Average Search Length，ASL）：在所有的查找过程中进行关键字的比较次数的平均值。
对于含有n个数据元素的查找表，查找成功的平均查找长度计算公式如下：
$$
ASL = \sum_{i=1}^{n}P_{i}C_{i}
$$
　　$P_i$：查找表中第i个数据元素的概率,一般等概率为$\frac{1}{n}$
　　$C_i​$：找到第i个数据元素时已经比较过的次数。

顺序查找

算法简介

顺序查找又称为线性查找，是一种最简单的查找方法。适用于线性表的顺序存储结构和链式存储结构。时间复杂度为$O（n）$。

基本思路

从第一个元素m开始逐个与需要查找的元素x进行比较，当比较到元素值相同(即m=x)时返回元素m的下标，如果比较到最后都没有找到，则返回-1。

优缺点

  • 缺点：当n 很大时，平均查找长度较大，效率低；
  • 优点：对表中数据元素的存储没有要求。另外，对于线性链表，只能进行顺序查找。

算法实现

1
2
3
4
5
6
7
8
9
//顺序查找，n为数组a的长度
int SequenceSearch(int a[], int value, int n)
{
    int i;
    for(i=0; i<n; i++)
        if(a[i]==value)
            return i;
    return -1;
}

折半查找

算法简介

折半查找，也称二分查找（Binary Search），是一种在有序数组中查找某一特定元素的查找算法。查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则查找过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。
这种查找算法每一次比较都使查找范围缩小一半。时间复杂度为$O（log_2^n）$。

基本思路
给予一个包含 n个带值元素的数组A
1、 令 L为0 ， R为 n-1 ；
2、 如果L>R，则搜索以失败告终 ；
3、 令 m (中间值元素)为 ⌊(L+R)/2⌋ (向下取整)；
4、 如果 $A_m<T$，令 L为 m + 1 并回到步骤二 ；
5、 如果 $A_m>T​$，令 R为 m - 1 并回到步骤二；

注意：
折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//二分查找（折半查找）,一般方法，n为数组a的长度
int BinarySearch1(int a[], int value, int n)
{
    int low, high, mid;
    low = 0;
    high = n-1;
    while(low<=high)
    {
        mid = (low+high)/2;
        if(a[mid]==value)             //取中间量
            return mid;
        else if(a[mid]>value)
            high = mid-1;            //从前半部分查找
        else
            low = mid+1;            //从后半部分查找
    }
    return -1;
}

//二分查找，递归方法
int BinarySearch2(int a[], int value, int low, int high)
{
    if(low>high)
        return -1;
    int mid = (low+high)/2;
    if(a[mid]==value)
        return mid;
    else if(a[mid]>value)
        return BinarySearch2(a, value, low, mid-1);
    else
        return BinarySearch2(a, value, mid+1, high);
}

插值查找

算法简介
在介绍插值查找之前，首先考虑一个新问题，为什么上述算法一定要是折半，而不是折四分之一或者折更多呢？
打个比方，在英文字典里面查“apple”，你下意识翻开字典是翻前面的书页还是后面的书页呢？如果再让你查“zoo”，你又怎么查？很显然，这里你绝对不会是从中间开始查起，而是有一定目的的往前或往后翻。
经过以上分析，折半查找这种查找方式，不是自适应的（也就是说是傻瓜式的）。二分查找中查找点计算如下：　
$$
mid=(low+high)/2, 即mid=low+1/2(high-low)
$$
通过类比，我们可以将查找的点改进为如下：
　　 mid=low+(key-a[low])/(a[high]-a[low])*(high-low)，
也就是将上述的比例参数1/2改进为自适应的，根据关键字在整个有序表中所处的位置，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。
查找成功或者失败的时间复杂度均为$O(log_2(log_2^n))$,最坏情况可能需要$O（n）$。
　
算法思想
基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，插值查找也属于有序查找。

注：对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
//插值查找，类似二分查找，只是mid计算方式不同，此处给出递归方法，一般方法也和上述二分查找类似
int InsertionSearch(int a[], int value, int low, int high)
{
    if(low>high)
        return -1;
    int mid = low+(value-a[low])/(a[high]-a[low])*(high-low);
    if(a[mid]==value)
        return mid;
    else if(a[mid]>value)
        return InsertionSearch(a, value, low, mid-1);
    else
        return InsertionSearch(a, value, mid+1, high);
}

分块查找

算法简介
要求是顺序表，分块查找又称索引顺序查找，它是顺序查找的一种改进方法。
时间复杂度：$O(log(m)+n/m)$

算法思想

  1. 将n个数据元素”按块有序”划分为m块（m ≤ n）。
  2. 每一块中的结点不必有序，但块与块之间必须”按块有序”；
  3. 即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；
  4. 而第2块中任一元素又都必须小于第3块中的任一元素，……

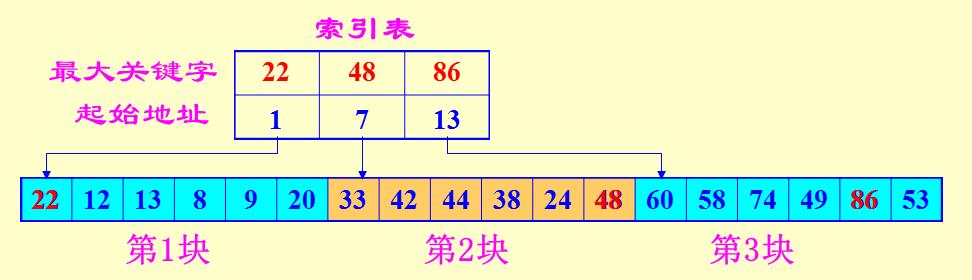
算法流程

  1. 先选取各块中的最大关键字构成一个索引表；
  2. 查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；
  3. 在已确定的块中用顺序法进行查找。

平均查找长度
将长度为n的查找表均匀分为m块，每块有s个记录，在等概率的情况，平均查找长度计算如下：

  1. 索引和块内均用顺序查找
    $$
    ASL= \frac{m+1}{2} + \frac{s+1}{2} = \frac{s^2+2s+n}{2s},(ms=n)
    $$
    特殊的
    $$
    当 s =\sqrt{n}时，ASL_{min} = \sqrt{n}+1
    $$

  2. 索引折半查找，块内顺序查找

$$
ASL = \left \lceil log_2^(m+1) \right \rceil + \frac{s+1}{2}
$$

斐波那契查找

这部分大致知道过程，先记录下来，以后有时间在认真研究一下=-=，主要参考百度百科

算法简介
斐波那契数列，又称黄金分割数列，指的是这样一个数列：$1、1、2、3、5、8、13、21、····$，在数学上，斐波那契被递归方法如下定义：$F(1)=1，F(2)=1，F(n)=f(n-1)+F(n-2) （n>=2）$。该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618）。

黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。

斐波那契查找的时间复杂度还是$O(log_2^n )$，但是与折半查找相比，斐波那契查找的优点是它只涉及加法和减法运算，而不用除法，而除法比加减法要占用更多的时间，因此，斐波那契查找的运行时间理论上比折半查找小，但是还是得视具体情况而定。

算法思想
也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。
相对于折半查找，一般将待比较的key值与第$mid=（low+high/2$位置的元素比较，比较结果分三种情况：

  1. 相等，mid位置的元素即为所求;
  2. 大于，$low=mid+1$;
  3. 小于，$high=mid-1$。

斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。要求开始表中记录的个数为某个斐波那契数小1，及$n=F(k)-1$;

开始将k值与第$F(k-1)$位置的记录进行比较(及$mid=low+F(k-1)-1$),比较结果也分为三种

  1. 相等，mid位置的元素即为所求
  2. 大于，$low=mid+1,k-=2$;

　　说明：$low=mid+1$说明待查找的元素在$[mid+1,high]$范围内，$k-=2$ 说明范围$[mid+1,high]$内的元素个数为$n-(F(k-1))= F(k)-1-F(k-1)=F(k)-F(k-1)-1=F(k-2)-1$个，所以可以递归的应用斐波那契查找。

  1. 小于，$high=mid-1,k-=1​$。

　　说明：$low=mid+1$说明待查找的元素在$[low,mid-1]$范围内，$k-=1$ 说明范围$[low,mid-1]$内的元素个数为$F(k-1)-1$个，所以可以递归 的应用斐波那契查找。
　　
$n=F(k)-1$， 表中记录的个数为某个斐波那契数小1。这是为什么呢？

是为了格式上的统一，以方便递归或者循环程序的编写。表中的数据是$F(k)-1$个，使用$mid$值进行分割又用掉一个，那么剩下$F(k)-2$个。正好分给两个子序列，每个子序列的个数分别是$F(k-1)-1$与$F(k-2)-1$个，格式上与之前是统一的。不然的话，每个子序列的元素个数有可能是$F(k-1)，F(k-1)-1，F(k-2)，F(k-2)-1$个，写程序会非常麻烦。

算法举例
对于斐波那契数列：$1、1、2、3、5、8、13、21、34、55、89……$（也可以从0开始），前后两个数字的比值随着数列的增加，越来越接近黄金比值0.618。比如这里的89，把它想象成整个有序表的元素个数，而89是由前面的两个斐波那契数34和55相加之后的和，也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段，那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618，假如要查找的元素在前半段，那么继续按照斐波那契数列来看，55 = 34 + 21，所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段，继续查找，如此反复，直到查找成功或失败，这样就把斐波那契数列应用到查找算法中了。

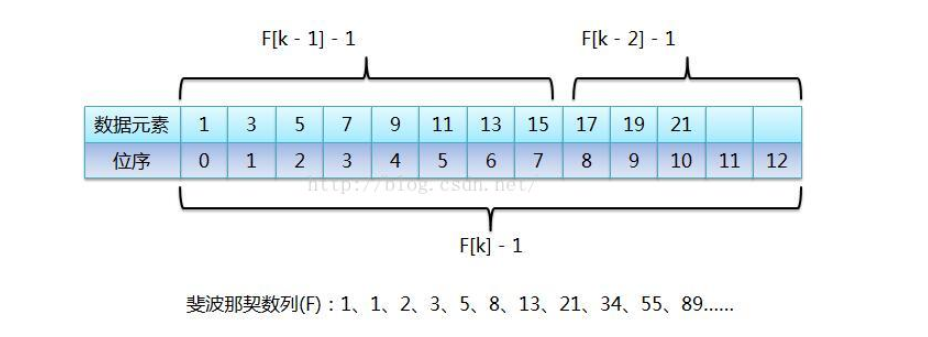
从图中可以看出，当有序表的元素个数不是斐波那契数列中的某个数字时，需要把有序表的元素个数长度补齐，让它成为斐波那契数列中的一个数值，当然把原有序表截断肯定是不可能的，不然还怎么查找。然后图中标识每次取斐波那契数列中的某个值时(F[k])，都会进行-1操作，这是因为有序表数组位序从0开始的，纯粹是为了迎合位序从0开始。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
// 斐波那契查找.cpp   
   
#include "stdafx.h"  
#include <memory>  
#include  <iostream>  
using namespace std;  
   
const int max_size=20;//斐波那契数组的长度  
   
/*构造一个斐波那契数组*/   
void Fibonacci(int * F)  
{  
    F[0]=0;  
    F[1]=1;  
    for(int i=2;i<max_size;++i)  
        F[i]=F[i-1]+F[i-2];  
}  
   
/*定义斐波那契查找法*/    
int Fibonacci_Search(int *a, int n, int key)  //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字  
{  
  int low=0;  
  int high=n-1;  
     
  int F[max_size];  
  Fibonacci(F);//构造一个斐波那契数组F   
   
  int k=0;  
  while(n>F[k]-1)//计算n位于斐波那契数列的位置  
      ++k;  
   
  int  * temp;//将数组a扩展到F[k]-1的长度  
  temp=new int [F[k]-1];  
  memcpy(temp,a,n*sizeof(int));  
   
  for(int i=n;i<F[k]-1;++i)  
     temp[i]=a[n-1];  
     
  while(low<=high)  
  {  
    int mid=low+F[k-1]-1;  
    if(key<temp[mid])  
    {  
      high=mid-1;  
      k-=1;  
    }  
    else if(key>temp[mid])  
    {  
     low=mid+1;  
     k-=2;  
    }  
    else  
    {  
       if(mid<n)  
           return mid; //若相等则说明mid即为查找到的位置  
       else  
           return n-1; //若mid>=n则说明是扩展的数值,返回n-1  
    }  
  }    
  delete [] temp;  
  return -1;  
}  
   
int _tmain(int argc, _TCHAR* argv[])  
{  
    int a[] = {0,16,24,35,47,59,62,73,88,99};  
    int key=100;  
    int index=Fibonacci_Search(a,sizeof(a)/sizeof(int),key);  
    cout<<key<<" is located at:"<<index;  
    system("PAUSE");  
    return 0;  
}

总结：本文主要介绍了5种常见的查找算法，在接下来的文章中，将继续介绍另外2种更重要的查找算法，树表查找和哈希查找。

------ 本文结束------
bluesliuf wechat
坚持技术分享，欢迎大家扫码交流！