上一篇博文主要介绍了哈希查找算法,本文主要介绍树表查找算法。这是一类算法,主要包含二叉查找树、平衡查找树之2-3查找树、平衡查找树之红黑树(Red-Black Tree)、B树和B+树。
本文主要弄懂各种查找树的思想,也附上了部分实现代码。代码有时间在详细研读,此处先记录下来。红黑树、B树和B+树还是有点难懂~ ~ ~,本文只是简要介绍了思想,具体实现见参考资料
二叉树查找算法
算法简介
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
算法思想
二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树。
二叉查找树性质:对二叉查找树进行中序遍历,即可得到有序的数列。
不同形态的二叉查找树如下图所示:
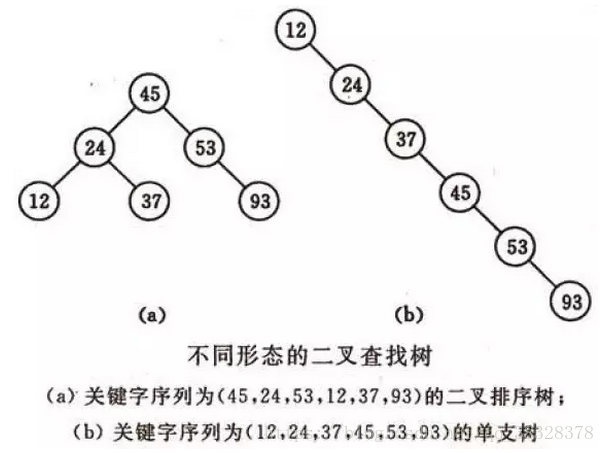
复杂度分析
它和二分查找一样,插入和查找的时间复杂度均为$O(logn)$,但是在最坏的情况下仍然会有$O(n)$的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。
查找过程
查找操作和二分查找类似,将key和节点的key比较,如果小于,那么就在Left Node节点查找,如果大于,则在Right Node节点查找,如果相等,直接返回Value。
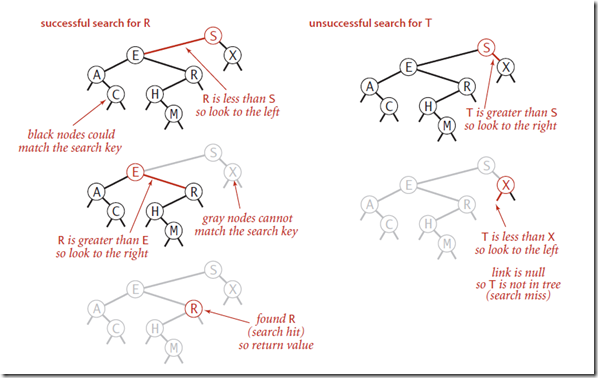
算法实现
本部分主要介绍两种二叉查找树的实现方式:递归和非递归。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33//非递归查找算法
BSTNode *BST_Search(BiTree T,ElemType key,BSTNode *&p){
//查找函数返回指向关键字值为key的结点指针,不存在则返回NULL
p=NULL;
while(T!=NULL&&key!=T->data){
p=T; //指向被查找结点的双亲
if(key<T->data)
T=T->lchild; //查找左子树
else
T=T->rchild; //查找右子树
}
return T;
}
//递归算法
Status Search_BST(BiTree T, int key, BiTree f, BiTree *p){
//查找BST中是否存在key,f指向T双亲,其初始值为NULL
//若查找成功,指针p指向数据元素结点,返回true;
//若失败,p指向查找路径上访问的最后一个结点并返回false
if(!T){
*p=f;
return false;
}
else if(key==T->data){ //查找成功
*p=T;
return true;
}
else if(key<T->data)
return Search_BST(T->lchild,key,T,p); //递归查找左子树
else
return Search_BST(T->rchild,key,T,p); //递归查找右子树
}
基于二叉查找树进行优化,可以得到其他的树表查找算法,如平衡树、红黑树等
平衡查找树之2-3查找树
平衡二叉树:BST中左右子树高度差的绝对值不超过1,平衡因子取值为{-1,0,1}
2-3查找树定义
和二叉树不一样,2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node),他保存1个key和左右两个自己点。对应3节点(3-node),保存两个Key,2-3查找树的定义如下:
- 要么为空,要么:
- 对于2节点,该节点保存一个key及对应value,以及两个指向左右节点的节点,左节点也是一个2-3节点,所有的值都比key要小,右节点也是一个2-3节点,所有的值比key要大。
- 对于3节点,该节点保存两个key及对应value,以及三个指向左中右的节点。左节点也是一个2-3节点,所有的值均比两个key中的最小的key还要小;中间节点也是一个2-3节点,中间节点的key值在两个跟节点key值之间;右节点也是一个2-3节点,节点的所有key值比两个key中的最大的key还要大。
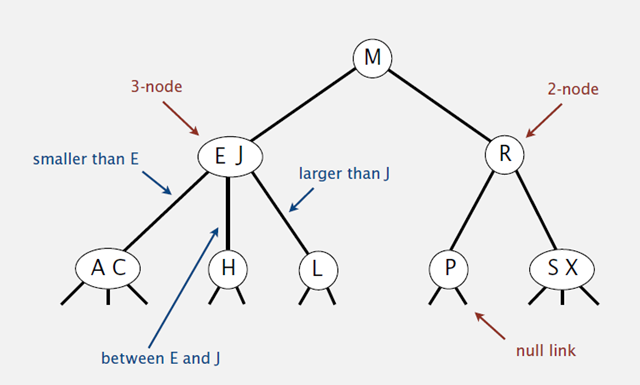
2-3查找树的性质
- 如果中序遍历2-3查找树,就可以得到排好序的序列;
- 在一个完全平衡的2-3查找树中,根节点到每一个为空节点的距离都相同。
复杂度分析
2-3树的查找效率与树的高度息息相关。
- 在最坏的情况下,也就是所有的节点都是2-node节点,查找效率为$log_2^N$
- 在最好的情况下,所有的节点都是3-node节点,查找效率为$log_3^N$约等于0.631$log_2^N$
对于插入来说,只需要常数次操作即可完成,因为他只需要修改与该节点关联的节点即可,不需要检查其他节点,所以效率和查找类似。
查找过程
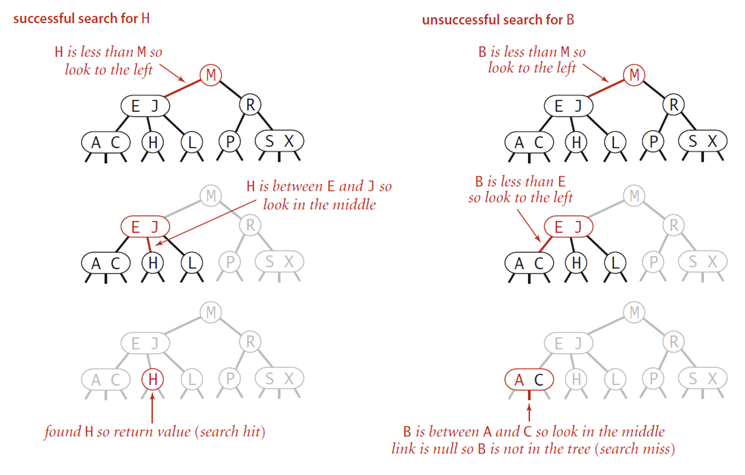
算法实现
直接实现2-3树比较复杂,因为:
- 需要处理不同的节点类型,非常繁琐
- 需要多次比较操作来将节点下移
- 需要上移来拆分4-node节点
- 拆分4-node节点的情况有很多种
2-3查找树实现起来比较复杂,在某些情况插入后的平衡操作可能会使得效率降低。在2-3查找树基础上改进的红黑树不仅具有较高的效率,并且实现起来较2-3查找树简单。
平衡查找树之红黑树(Red-Black Tree)
2-3查找树能保证在插入元素之后能保持树的平衡状态,最坏情况下即所有的子节点都是2-node,树的高度为lgn,从而保证了最坏情况下的时间复杂度。但是2-3树实现起来比较复杂,于是就有了一种简单实现2-3树的数据结构,即红黑树(Red-Black Tree)。
基本思想
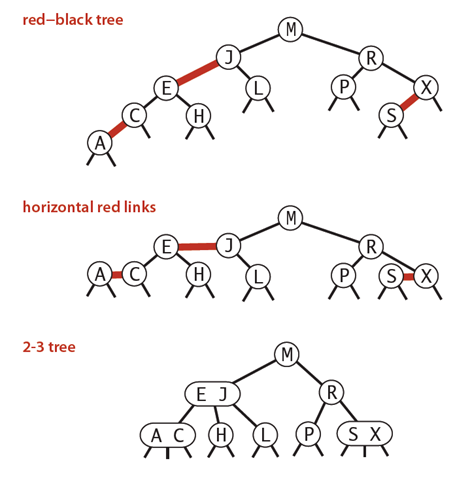
红黑树的思想就是对2-3查找树进行编码,尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型,红色链接,他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的,使用红色链接的两个2-nodes来表示一个3-nodes节点,并且向左倾斜,即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改,和普通的二叉查找树相同。
基本定义
红黑树是一种具有红色和黑色链接的平衡查找树,同时满足:
- 红色节点向左倾斜
- 一个节点不可能有两个红色链接
- 整个树完全黑色平衡,即从根节点到所以叶子结点的路径上,黑色链接的个数都相同。
下图可以看到红黑树其实是2-3树的另外一种表现形式:如果我们将红色的连线水平绘制,那么他链接的两个2-node节点(E和J)就是2-3树中的一个3-node节点了。
性质
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制的一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
下面是一个具体的红黑树的图例:

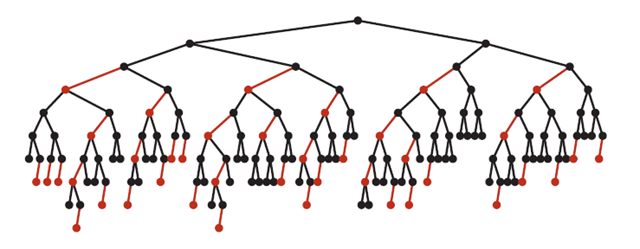
复杂度分析:最坏的情况就是,红黑树中除了最左侧路径全部是由3-node节点组成,即红黑相间的路径长度是全黑路径长度的2倍。
下图是一个典型的红黑树,从中可以看到最长的路径(红黑相间的路径)是最短路径的2倍:
B树
B树(B-tree),也称多路平衡查找树,是一种树状数据结构,能够用来存储排序后的数据。这种数据结构能够让查找数据、循序存取、插入数据及删除的动作,都在对数时间内完成。B树,概括来说是一个一般化的二叉查找树,可以拥有多于2个子节点。
B树的定义
B树作为一种多路搜索树(并不是二叉的),B树中所有结点的孩子结点数的最大值成为B树的阶,通常记做M。
- 树中每个结点至多有M棵子树,(M>2);
- 若根结点不是终端结点,则其子树数目为$[2, M]$;
- 除根结点以外的非叶子结点的子树数目为$[\lceil M/2 \rceil, M]$(向上取整);
- 每个结点存放至少$\lceil M/2 \rceil-1$和至多$M-1$个关键字;
- 非叶子结点的关键字个数=指向子树的指针个数-1;
- 非叶子结点的关键字:$K[1], K[2], …, K[M-1]$;且$K[i] < K[i+1]$;
- 非叶子结点的指针:$P[1], P[2], …, P[M]$;其中$P[1]$指向关键字小于$K[1]$的子树,$P[M]$指向关键字大于$K[M-1]$的子树,其它$P[i]$指向关键字属于($K[i-1], K[i]$)的子树;
- 所有叶子结点位于同一层;
对于任意一棵包含n个关键字,高度为h,阶数为m的B树,其高度满足:
B树的高度:$log_{m}^{n+1}\leq h \leq log_{\lceil m/2 \rceil}^{[(n+1)/2]}+1$
下图是一个M=3 阶的B树:
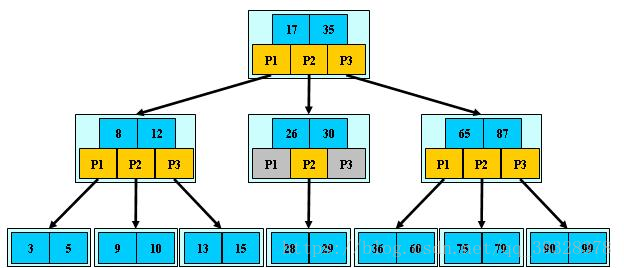
B树的构造
可以看到B树是2-3树的一种扩展,他允许一个节点有多于2个的元素。B树的插入及平衡化操作和2-3树很相似,这里就不介绍了。下面是往B树中依次插入
6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4
的演示动画(https://files-cdn.cnblogs.com/files/yangecnu/btreebuild.gif):
最后结果如下:
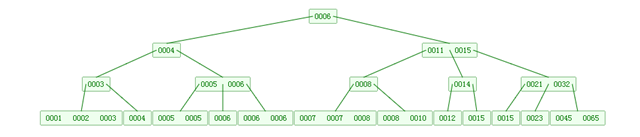
B树的查找
在B树中查找给定关键字的方法是,首先把根结点取来,在根结点所包含的关键字$K_1,…,K_n$查找给定的关键字(可用顺序查找或二分查找法),若找到等于给定值的关键字,则查找成功;否则,一定可以确定要查找的关键字在$K_i与K_{i+1}$之间,$P_i$为指向子树根节点的指针,此时取指针$P_i$所指的结点继续查找,直至找到,或指针$P_i$为空时查找失败。
B-树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程,从而加快存取速度。这种数据结构常被应用在数据库和文件系统的实作上。
B+树
B+树是应数据库所需出现的一种B树的变形树。
定义
一棵M阶的B+树需满足以下条件:
- 其定义基本与B-树相同,除了:
- 非叶子结点的子树指针与关键字个数相同;
- 非叶子结点的子树指针$P[i]$,指向关键字值属于$[K[i], K[i+1])$的子树(B-树是开区间);
- 为所有叶子结点增加一个链指针;
- 所有关键字都在叶子结点出现;
下图是一个M=3 阶的B+树:
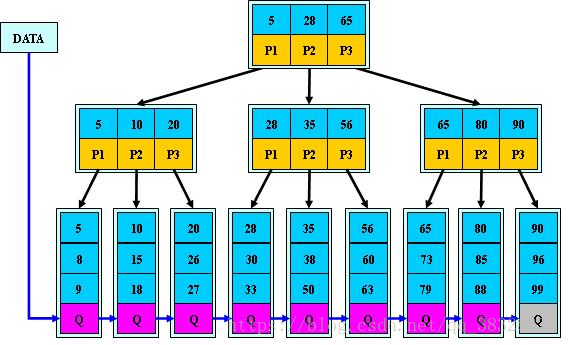
B树的构造
(https://files-cdn.cnblogs.com/files/yangecnu/Bplustreebuild.gif) 为一个B+树创建的示意图:
最后结果如下:
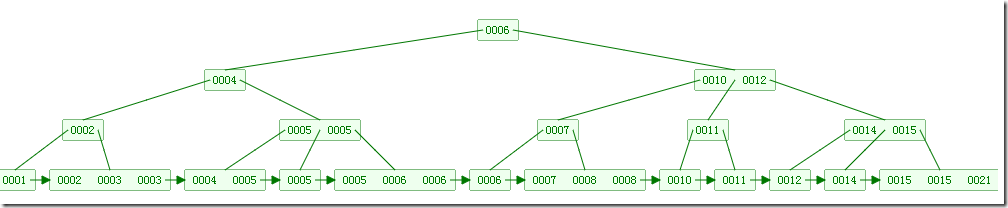
B+树的查找
B+树的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B树与B+树的对比
B和B+树的区别在于,B+树的非叶子结点只包含导航信息,不包含实际的值,所有的叶子结点和相连的节点使用链表相连,便于区间查找和遍历。
B树的优点
由于B树的每一个节点都包含key和value,因此经常访问的元素可能离根节点更近,因此访问也更迅速。
B+树的优点
- 由于B+树在内部节点上不好含数据信息,因此在内存页中能够存放更多的key。 数据存放的更加紧密,具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。
- B+树的叶子结点都是相链的,因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻,所以缓存命中性没有B+树好。
下面是B 树和B+树的区别图:
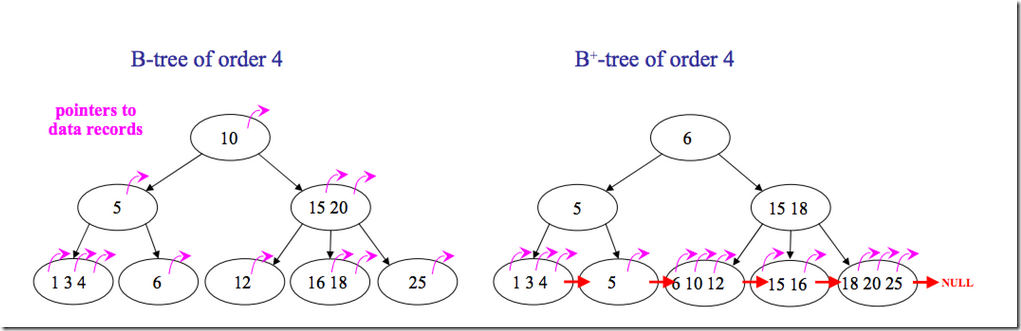
总结
二叉查找树平均查找性能不错,为$O(logn)$,但是最坏情况会退化为$O(n)$。在二叉查找树的基础上进行优化,我们可以使用平衡查找树。平衡查找树中的2-3查找树,这种数据结构在插入之后能够进行自平衡操作,从而保证了树的高度在一定的范围内进而能够保证最坏情况下的时间复杂度。但是2-3查找树实现起来比较困难,红黑树是2-3树的一种简单高效的实现,他巧妙地使用颜色标记来替代2-3树中比较难处理的3-node节点问题。红黑树是一种比较高效的平衡查找树,应用非常广泛,很多编程语言的内部实现都或多或少的采用了红黑树。
除此之外,2-3查找树的另一个扩展——B/B+平衡树,在文件系统和数据库系统中有着广泛的应用。
