本文主要介绍树和二叉树的应用,主要包含3个部分:二叉排序树、平衡二叉树和哈夫曼树和哈夫曼编码。
二叉排序树(BST)
定义
二叉排序树(简称BST),也称二叉查找树。二叉排序树或者是一棵空树,或者是一棵有下列特性的非空二叉树:
- 若左子树非空,则左子树上所有结点关键字的值均小于根结点的关键字值
- 若右子树非空,则右子树上所有结点关键字的值均大于根结点的关键字值
- 左、右子树本身也分别是一棵二叉排序树
查找
关于二叉排序的查找,在C语言实现七大查找算法(三)我的这篇博文中,已经详细介绍了,此处不再赘述。
查找效率:平均查找长度主要取决于树的高度。
二叉排序树和二分查找的对比
| 二叉排序树 | 二分查找(有序顺序表) | |
|---|---|---|
| 判定树 | 不唯一 | 唯一 |
| 有序性 | 无需移动结点,修改指针 | |
| 插入、删除 | $O(log_2^n)$ | $O(n)$ |
| 有序表静态 | √ | |
| 有序表动态 | √ |
插入
二叉排序树作为一种动态集合,特点是树的结构不是一次生成的,而是在查找过程中当树中不存在关键字给定值的结点时在进行插入。
由于二叉排序树是递归定义的,插入结点的过程如下:
- 若原二叉排序树为空,直接插入结点
- 若关键字$k$小于根结点的关键字,插入到左子树中
- 若关键字$k$大于根结点的关键字,插入到右子树中
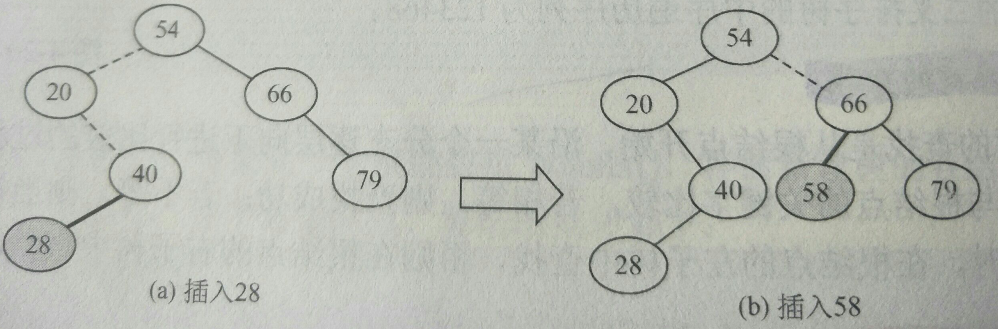
一个插入示例如下(插入28,58),发现插入的新结点一定是某个叶子结点。
实现代码如下1
2
3
4
5
6
7
8
9
10
11
12
13
14int BST_InSert(BiTree &T,KeyType k){
if(T==NULL){ //原树为空,新插入的记录为根结点
T=(BiTree) malloc (sizeof(BSTNode));
T->key=k;
T->lchild=T->rchild=NULL;
return 1;
}
else if(k==T->key) //树中存在相同关键字的结点
return 0;
else if(k<T->key)
return BST_InSert(T->lchild,k); //递归插入T的左子树中
else
return BST_InSert(T->rchild,k); //递归插入T的右子树中
}
构造
1 | void Creat_BST(BiTree &T,KeyType str[],int n){ |
删除
在二叉排序树中删除一个结点时,不能把以该结点为根的子树上的结点都删除,必须先把被删除结点从存储二叉排序树的链表上摘下,将因删除结点而断开的二叉链表重新链接起来,同时确保二叉排序树的性质不会丢失。
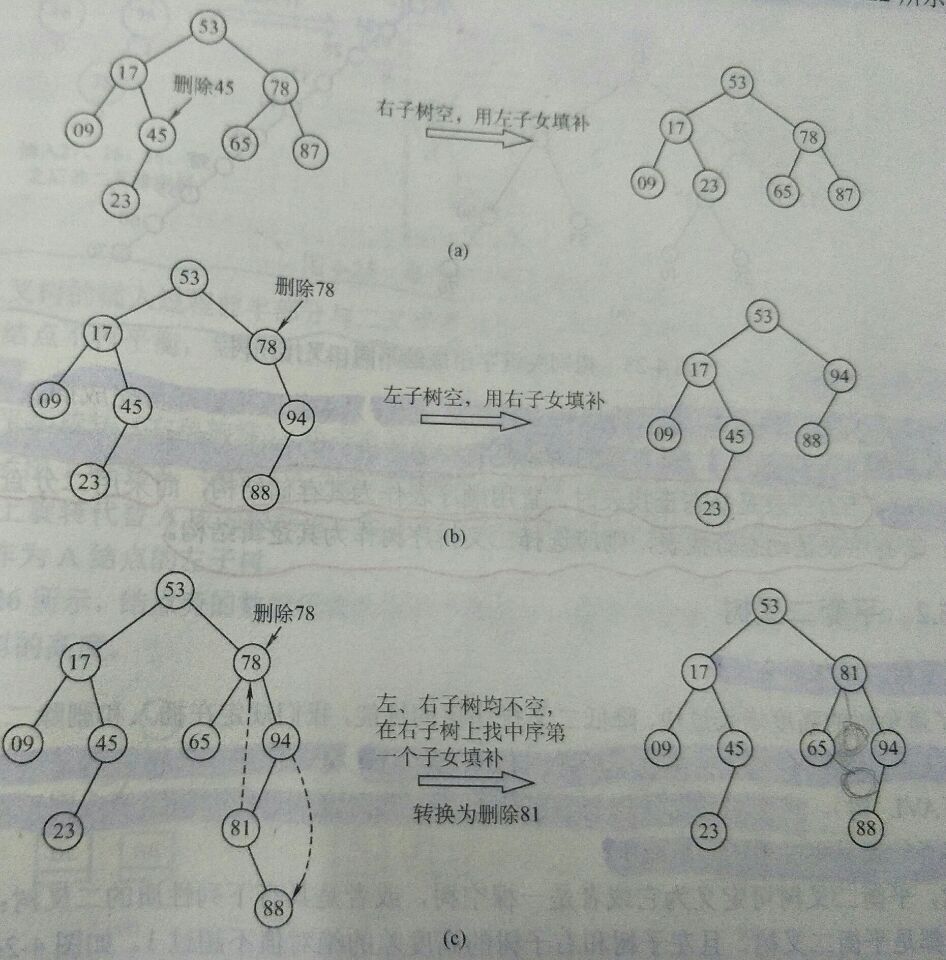
删除操作实现过程按以下3种情况来处理:
- 若删除的结点z为叶子结点,直接删除
- 若结点$z$只有一颗左子树或右子树,则让$z$的子树成为$z$父节点的子树,替代$z$的位置
- 若$z$有左右2棵子树,则令$z$的直接后继(或直接前驱)替代$z$,然后从$BST$中删去这个直接后继(或直接前驱),这样就转化为了第一种或第二种情况
删除示例如下:
平衡二叉树(AVL)
定义
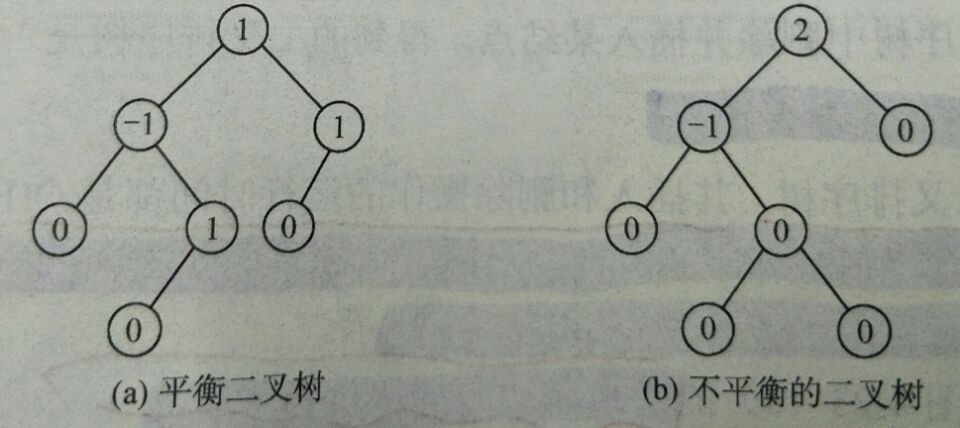
为了避免树的高度增长过快,降低二叉排序树的性能,我们规定在插入和删除二叉树结点时,要保证任意结点的左、右子树高度差的绝对值不超过1,将这样的树称为平衡二叉树。
平衡因子:结点左子树和右子树的高度差,取值只可能为$-1,0,1$。
平衡二叉树示例图
插入
- 未破坏平衡,无需调整
- 破坏平衡,先找到插入路径上离插入结点最近的平衡因子绝对值大于1的结点A,再对以A为根的子树,调整各结点的位置关系,使之重新达到平衡。
示例图如下,其中75即为A结点
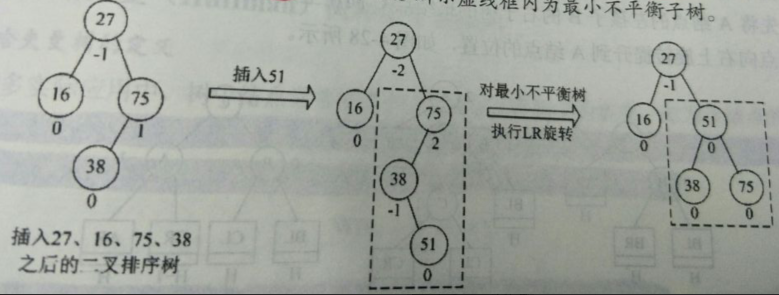
平衡二叉树的插入过程前半部分与二叉排序树相同,但是在插入新结点后,如果造成了不平衡,要做出相应的调整,可以归纳为以下4种调整情况:
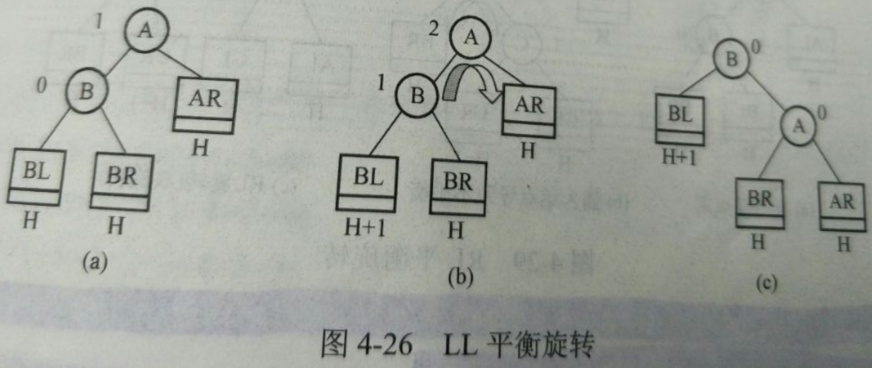
- LL(右单旋转)在A的左孩子的左子树上插入新结点。将A的左孩子B向右上旋转替代A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。
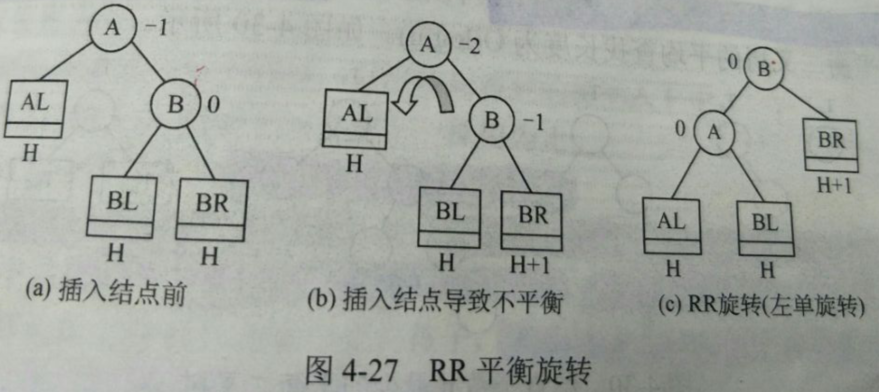
- RR(左单旋转)在A的右孩子的右子树上插入新结点。将A的右孩子B向左上旋转替代A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A结点的右子树。
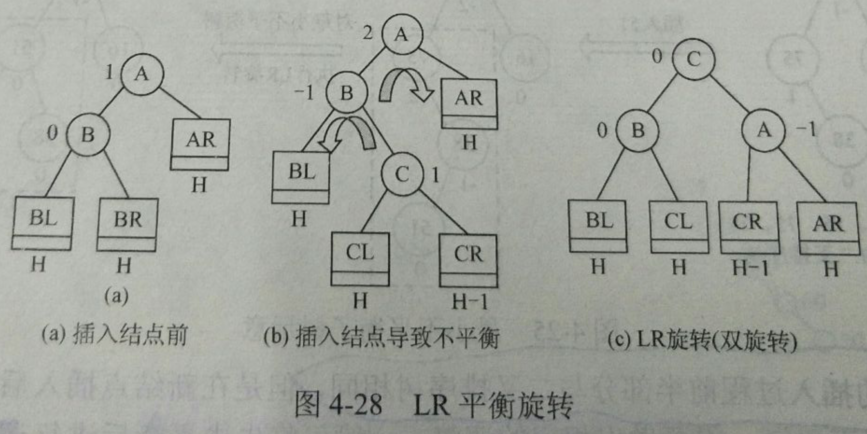
- LR(先左后右)在A的左孩子的右子树上插入新结点。先将A的左孩子B的右子树的根结点C向左上旋转提升到B的位置,然后再把该C结点向右上旋转提升到A的位置。
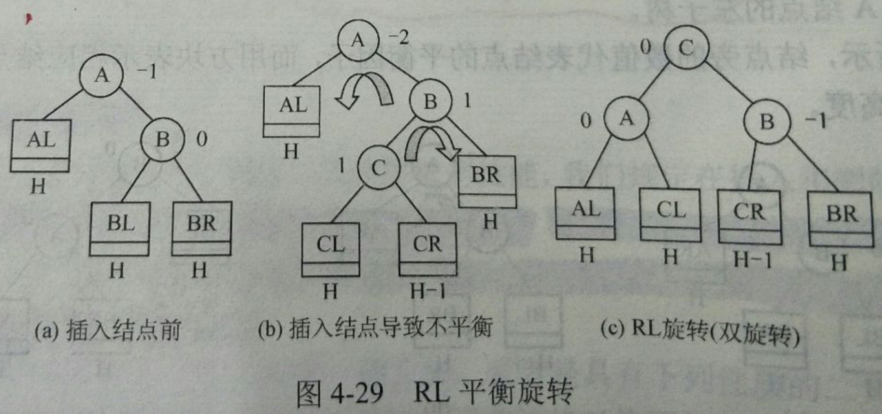
- RL(先右后左)在A的右孩子的左子树上插入新结点。先将A的右孩子B的左子树的根结点C向右上旋转提升到B的位置,然后再把该C结点向左上旋转提升到A的位置。
查找
平衡二叉树的查找过程和二叉排序树相同。假设$N_h$表示深度为$h$的$AVL$中含有的最少结点数,显然$N_0=1,N_1=2,N_h=N_{h-1}+N_{h-2}+1$。
结论:$n$个结点的平衡二叉树的最大深度为$log_2^n$,平均查找长度为$O(log_2^n)$。
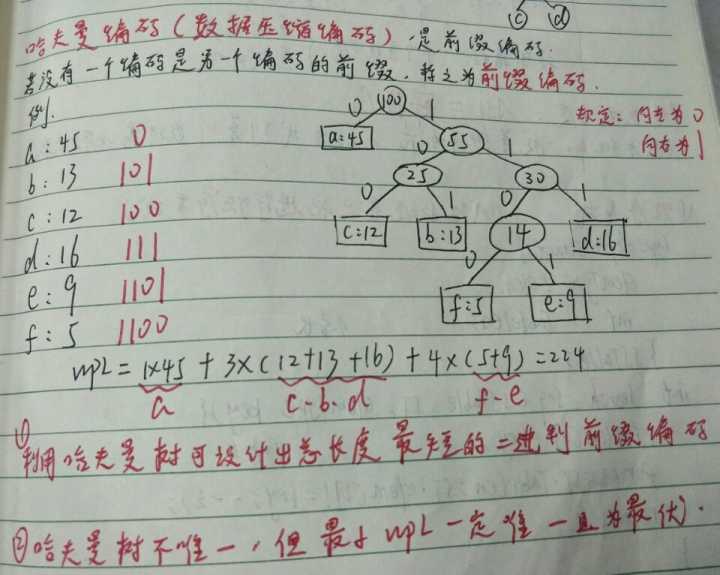
哈夫曼(Huffman)树和哈夫曼编码
哈夫曼树
定义和构造

示例
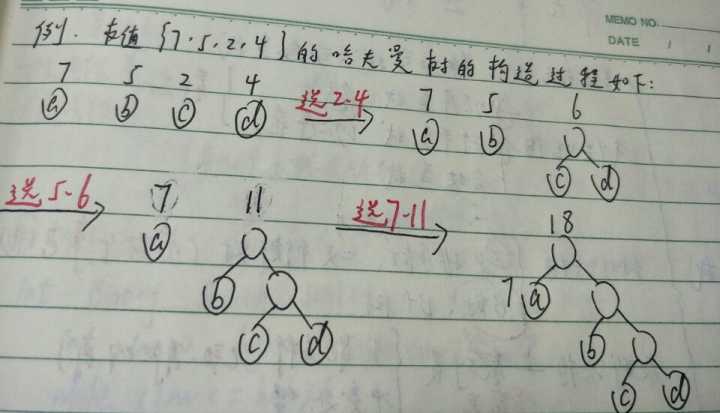
哈夫曼编码