机器学习方法之K-means聚类

聚类(Clustering)，就是将相似的事物聚集在一 起，而将不相似的事物划分到不同的类别的过程，是数据分析之中十分重要的一种手段。与此前介绍的决策树，支持向量机等监督学习不同，聚类算法是非监督学习(unsupervised learning )，在数据集中，并不清楚每条数据的具体类别。

算法

K-means 算法是数据挖掘十大经典算法之一。由于该算法的效率高，所以在对大规模数据进行聚类时被广泛应用。目前，许多算法均围绕着该算法进行扩展和改进。

k-means 算法接受一个参数 k ，表示将数据集中的数据分成 k 个聚类。在同一个聚类中，数据的相似度较高；而不同聚类的数据相似度较低。

算法的步骤：
1. 选择任意 k 个数据，作为各个聚类的质心，（质心也可以理解为中心的意思），执行步骤 2；
2. 对每个样本进行分类，将样本划分到最近的质心所在的类别（欧氏距离），执行步骤 3；
3. 取各个聚类的中心点作为新的质心，执行步骤 2 进行迭代。

迭代结束的条件：
1. 当新的迭代后的聚类结果没有发生变化；
2. 当迭代次数达到预设的值。

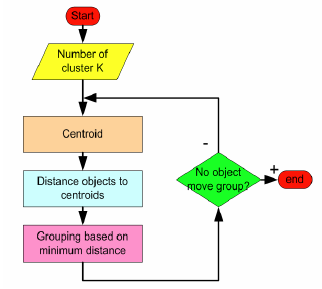
算法流程图：

实例分析

有如下4种药物，我们要根据其2个特征值对其进行分类，事先并不知道它们属于何种类别。聚类后分为2类（1 和 2）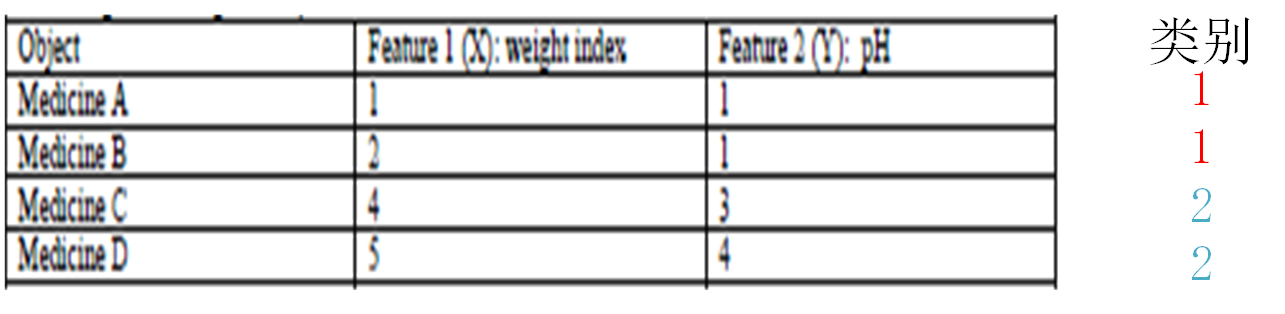

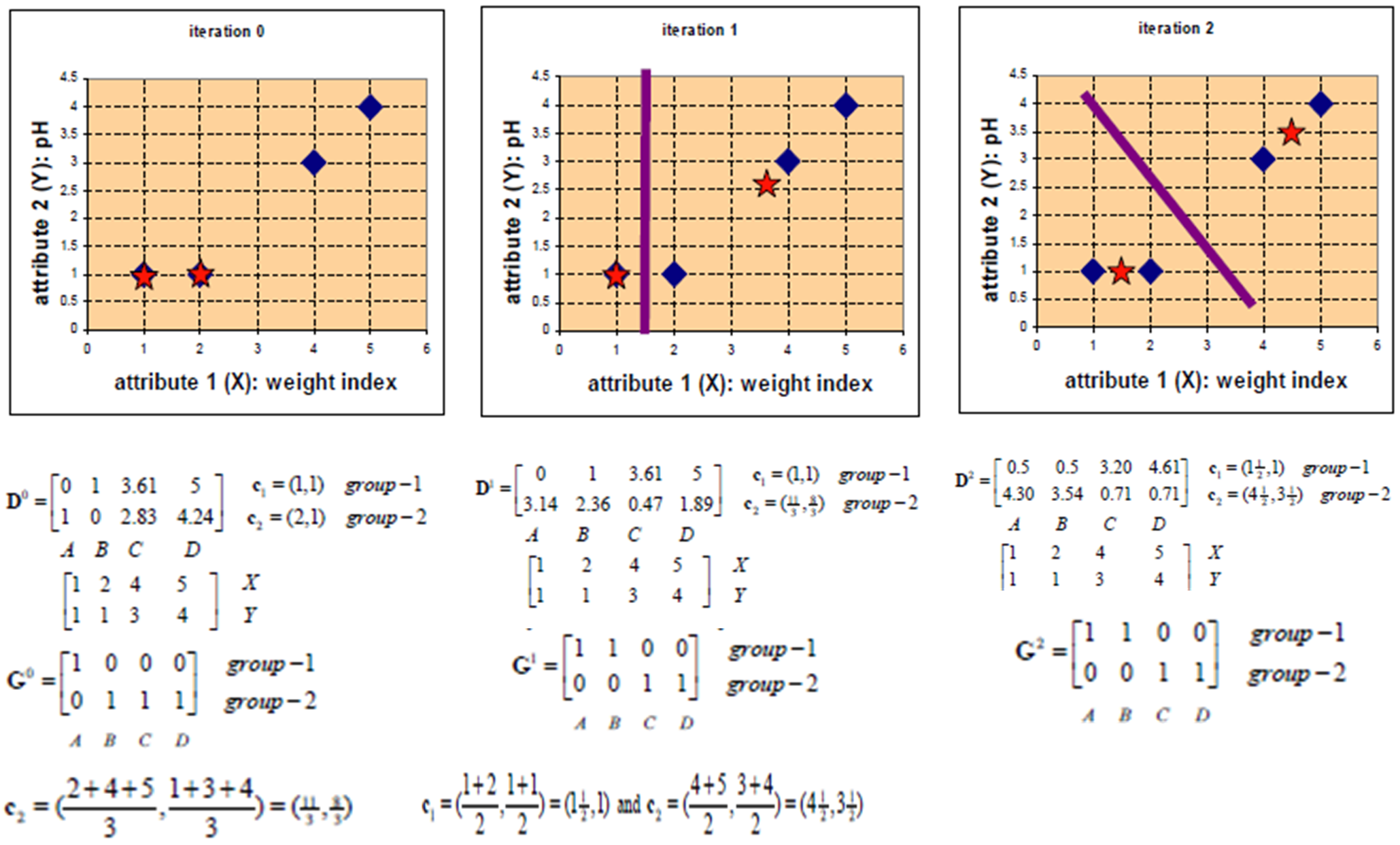
按照之前的算法流程，我们将4种药划分为了2类，聚类过程如下：

代码实现

本部分我们将使用和上面实例分析中一致的数据，采用2种方法实现k-means聚类。

自己实现

代码主要包含4个小方法，分别是：

1. shouldStop()：聚类迭代的终止条件
2. updateLabels()：更新迭代后数据的类标签
3. getLabelFromClosestCenterpoints()：计算各数据到中心点的距离，选取最近距离更新数据类标签
4. getCenterpoints()：根据聚类结果选取新的中心点

   import numpy as np
   
   def kmeans(x,k,maxIt):
       '''
       :param x: 待分类数据
       :param k: 最终分为几类
       :param maxIt: 最大迭代次数
       :return: 分好类的数据
       '''
       numpoints,numDim = x.shape #数据行数和列数
       dataSet = np.zeros((numpoints,numDim+1)) # 创建一个新数组存储分类好的数据
       dataSet[:,:-1] = x # 将数据x赋值给dataSet的前n-列
   
       centerpoints = dataSet[np.random.randint(numpoints,size=k),:] # 随机选取k个中心点
       centerpoints = dataSet[0:2, :] # 强制选取前2条数据作为中心点，为了对照实例分析
       centerpoints[:,-1] = range(1,k+1) # 为选好的中心点数据打上标签
   
       iterations = 0 # 迭代次数
       oldCenterpoints = None
   
       # 调用函数循环迭代，实现聚类
       while not shouldStop(oldCenterpoints,centerpoints,iterations,maxIt):
           # 输出每次迭代的聚类过程
            print("iterations: \n",iterations)
            print("dataSet: \n",dataSet)
            print("centerpoints: \n",centerpoints)
           # 将原始中心点复制存储，方便迭代完后，比较新旧中心点是否发生变化
            oldCenterpoints =np.copy(centerpoints)
            iterations += 1
           # 调用方法更新每条数据的类标签
            updateLabels(dataSet,centerpoints)
           # 根据每一次迭代后的聚类结果，重新选取新的中心点
            centerpoints = getCenterpoints(dataSet,k)
   
       return dataSet
   
   # 聚类迭代的终止条件
   def shouldStop(oldCenterpoints,centerpoints,iterations,maxIt):
       '''
       :param oldCenterpoints: 迭代前的中心点
       :param centerpoints: 迭代后的中心点
       :param iterations: 当前迭代次数
       :param maxIt: 最大迭代次数
       :return: True或False
       '''
       if iterations > maxIt: # 超出设定好的最大迭代次数
           return True
       return np.array_equal(oldCenterpoints,centerpoints) # 判断迭代前后中心点是否发生了变化
   
   # 更新迭代后数据的类标签
   def updateLabels(dataSet,centerpoints):
       '''
       :param dataSet: 数据
       :param centerpoints: 中心点
       '''
       numpoints,numDim = dataSet.shape
       for i in range(0,numpoints):
           # 调用方法循环更新数据的类标签
           dataSet[i,-1] = getLabelFromClosestCenterpoints(dataSet[i,:-1],centerpoints)
   
   # 根据计算各数据到中心点的距离，选取最近距离更新数据类标签
   def getLabelFromClosestCenterpoints(dataSetRow,centerpoints):
       '''
       :param dataSetRow: 待更新类标签的数据
       :param centerpoints: 中心点
       :return: 数据新的类标签
       '''
       label = centerpoints[0,-1] # 选取初始类标签
       minDist = np.linalg.norm(dataSetRow - centerpoints[0,:-1]) # 计算和当前中心点的距离
       # 循环计算数据和每个中心点的距离，选取最近的更新类标签
       for i in range(1,centerpoints.shape[0]):
           dist =  np.linalg.norm(dataSetRow - centerpoints[i,:-1]) # 计算距离
           if dist < minDist:
               minDist = dist
               label = centerpoints[i,-1]
       print("minDist: ",minDist)
       return label
   
   # 根据聚类结果选取新的中心点
   def getCenterpoints(dataSet,k):
       '''
       :param dataSet: 数据
       :param k: 最终分为几类
       :return: 新的中心点
       '''
       result = np.zeros((k,dataSet.shape[1]))
       for i in range(1,k+1):
           oneCluster = dataSet[dataSet[:,-1]==i,:-1] # 同类数据按行求均值，算出新的中心点
           result[i-1,:-1] = np.mean(oneCluster,axis=0)
           result[i-1,-1] = i # 打上标签
       return result
   
   # 创建测试数据
   x1 = np.array([1,1])
   x2 = np.array([2,1])
   x3 = np.array([4,3])
   x4 = np.array([5,4])
   test_x = np.vstack((x1,x2,x3,x4)) #沿着列方向将矩阵堆叠起来
   result = kmeans(test_x,2,10)
   print("final result: \n",result)

程序运行结果如下：

iterations: 
 0
dataSet: 
 [[1. 1. 1.]
 [2. 1. 2.]
 [4. 3. 0.]
 [5. 4. 0.]]
centerpoints: 
 [[1. 1. 1.]
 [2. 1. 2.]]
minDist:  0.0
minDist:  0.0
minDist:  2.8284271247461903
minDist:  4.242640687119285
iterations: 
 1
dataSet: 
 [[1. 1. 1.]
 [2. 1. 2.]
 [4. 3. 2.]
 [5. 4. 2.]]
centerpoints: 
 [[1.         1.         1.        ]
 [3.66666667 2.66666667 2.        ]]
minDist:  0.0
minDist:  1.0
minDist:  0.4714045207910319
minDist:  1.885618083164127
iterations: 
 2
dataSet: 
 [[1. 1. 1.]
 [2. 1. 1.]
 [4. 3. 2.]
 [5. 4. 2.]]
centerpoints: 
 [[1.5 1.  1. ]
 [4.5 3.5 2. ]]
minDist:  0.5
minDist:  0.5
minDist:  0.7071067811865476
minDist:  0.7071067811865476
final result: 
 [[1. 1. 1.]
 [2. 1. 1.]
 [4. 3. 2.]
 [5. 4. 2.]]

通过比较，可以发现结果和我们在实例分析中的一致。

Sklearn实现

from sklearn import cluster
import numpy as np

# 创建测试数据
x1 = np.array([1,1])
x2 = np.array([2,1])
x3 = np.array([4,3])
x4 = np.array([5,4])
test_x = np.vstack((x1,x2,x3,x4)) #沿着列方向将矩阵堆叠起来

sk = cluster.KMeans(2)
sk.fit(test_x)
print("中心点：\n",sk.cluster_centers_)
print("类别：\n",sk.labels_)

程序运行结果如下：

中心点：
 [[4.5 3.5]
 [1.5 1. ]]
类别：
 [1 1 0 0]

最后的中心点一致，也成功分为了2类

优缺点

优点：

1. 速度快，复杂度低，为 O(Nkq)，N是数据总量，k是类别数，q是迭代次数。一般来讲k、q会比N小得多，那么此时复杂度相当于O(N) ，在各种算法中是算很小的；
2. 原理简单，易于理解。

缺点：

1. 对异常点敏感；
2. 局部最优解而不是全局优，(分类结果与初始点选取有关);
   不能发现非凸形状的聚类。

K-means++算法

2007年由D. Arthur等人提出的K-means++算法在k-means的基础上做了进一步的改进。可以直观地将这改进理解成这K个初始聚类中心相互之间应该分得越开越好。整个算法的描述如下图所示：

下面结合一个简单的例子说明K-means++是如何选取初始聚类中心的。数据集中共有8个样本，分布以及对应序号如下图所示：

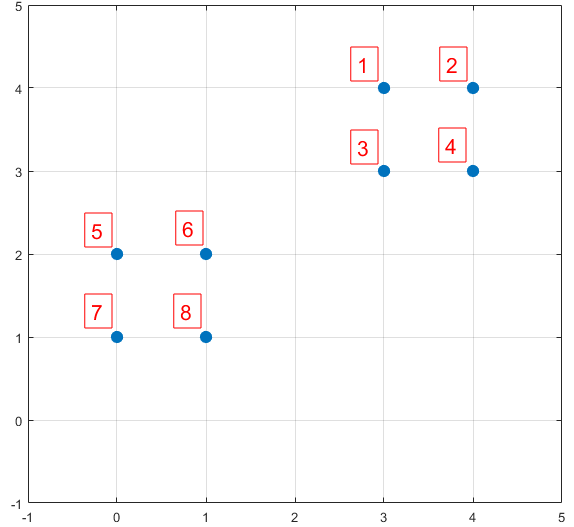
假设经过图2的步骤一后6号点被选择为第一个初始聚类中心，那在进行步骤二时每个样本的D(x)和被选择为第二个聚类中心的概率如下表所示：

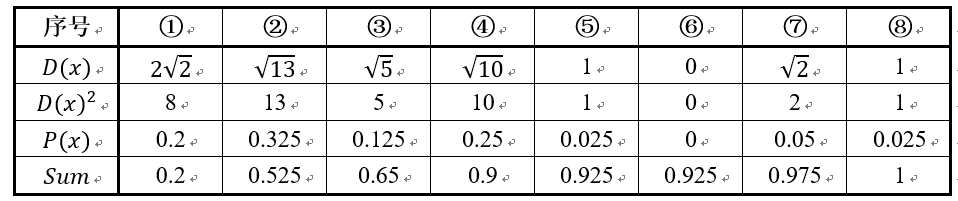
其中的$P(x)$就是每个样本被选为下一个聚类中心的概率。最后一行的$Sum$是概率$P(x)$的累加和，用于轮盘法选择出第二个聚类中心。方法是随机产生出一个0~1之间的随机数，判断它属于哪个区间，那么该区间对应的序号就是被选择出来的第二个聚类中心了。例如1号点的区间为[0,0.2)，2号点的区间为[0.2, 0.525)。

从上表可以直观的看到第二个初始聚类中心是1号，2号，3号，4号中的一个的概率为0.9。而这4个点正好是离第一个初始聚类中心6号点较远的四个点。这也验证了K-means的改进思想：即离当前已有聚类中心较远的点有更大的概率被选为下一个聚类中心。可以看到，该例的K值取2是比较合适的。当K值大于2时，每个样本会有多个距离，需要取最小的那个距离作为$D(x)​$。