机器学习方法之非线性回归（ Logistic Regression）

发表于 | 更新于 | 分类于 | 阅读次数
字数统计 1.6k | 阅读时长 6

非线性回归是线性回归的延伸，其目标预测函数不是线性的。本文主要介绍逻辑回归（Logistic Regression），它是非线性回归的一种，虽然名字中有“回归”二字，但其本质上是一个分类模型。

含义

我们知道，线性回归的模型是求出输出特征向量Y和输入样本矩阵X之间的线性关系系数θ，满足$Y=Xθ$。此时Y是连续的，所以是回归模型。如果Y是离散的话，如何解决？一个可以想到的办法是，我们对于Y再做一次函数转换，变为g(Y)。如果我们令g(Y)的值在某个实数区间的时候是类别A，在另一个实数区间的时候是类别B，以此类推，就得到了一个分类模型。如果结果的类别只有两种，那么就是一个二元分类模型了。逻辑回归的出发点就是从这来的。

看如下实例
有这么几组医疗数据，X特征是肿瘤的大小（连续型），Y是其良恶性（离散型），Y只有0（良性）和1（恶性）2种取值。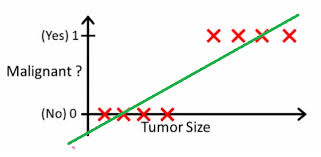

我们选取阈值0.5，h（x）>0.5（恶性），Malignant=1，反之为0，良性。


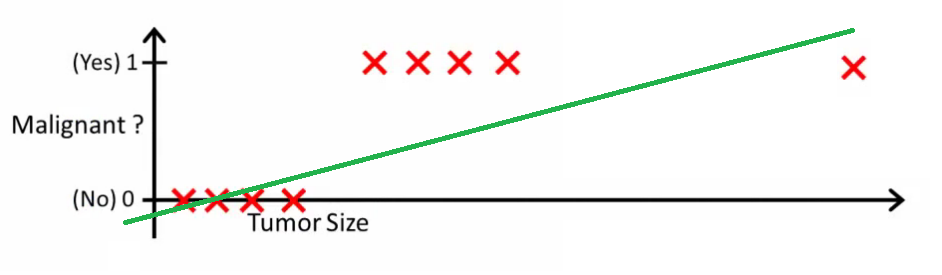
我们选取阈值0.2，h（x）>0.2（恶性），Malignant=1，反之为0，良性。

比较上述两种情况，新的数值加入时需要不断调整阈值，说明用线性的方法进行回归不太合理。

基本模型

我们假设测试数据为$X(x_0,x_1,…,x_n)$
需要学习的参数为$\Theta(\theta_0,\theta_1,…,\theta_n)$

给定函数

$$
Z = \theta_0 + \theta_1x_1 + \theta_2x_2+…+\theta_nx_n
$$
向量化可表示为
$$
Z = \Theta^TX
$$
经常需要一个分界线作为区分两类结果。再次需要一个函数进行曲线平滑化，由此引入Sigmoid 函数进行转化：

$$
g(z) = \frac{1}{1+e^{-z}}
$$

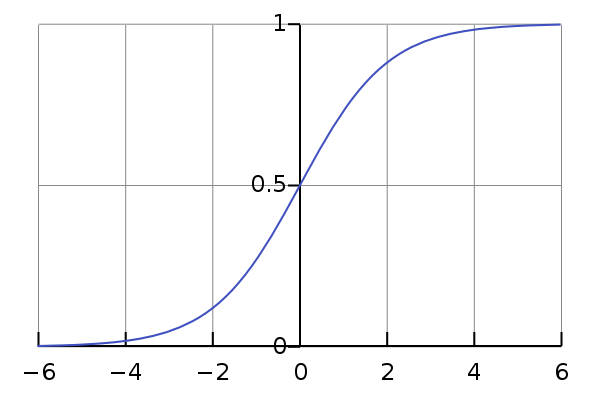
这样的，可以以 0.5 作为分界线。因此逻辑回归的最终目标函数就是：
$$
h_\theta(X) = g(\theta_0 + \theta_1x_1 + \theta_2x_2+…+\theta_nx_n) = g(\theta^TX) = \frac{1}{1+e^{-\theta^TX}}
$$
回归是用来得到样本属于某个分类的概率。因此在分类结果中，假设 y 值是 0 或 1，那么正例 (y = 1):

$$
h_\theta(X) = P(y=1|X;\theta)
$$
反例(y = 0):
$$
1 - h_\theta(X) = P(y=0|X;\theta)
$$
在线性回归中，我们要找到合适的$\theta^{(i)}$使下面的损失函数值最小：
$$
Cost(h_\theta(x^{(i)}),y^{(i)}) = \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2
$$
如果在逻辑回归中运用上面这种损失函数，得到的函数 J 是一个非凸函数，存在多个局部最小值，很难进行求解，因此需要换一个 cost 函数。重新定义个 cost 函数如下：
$$
Cost(h_\theta(x^{(i)}),y^{(i)}) = -\frac{1}{m}[\sum_{i=1}^{m}(y^{(i)}log(h_\theta(x^{(i)})) + (1-y^{(i)})log(1-h_\theta(x^{(i)})))]
$$

求解方法

我们采用梯度下降法求解最佳解。梯度下降法的计算过程就是沿梯度下降的方向求解极小值。

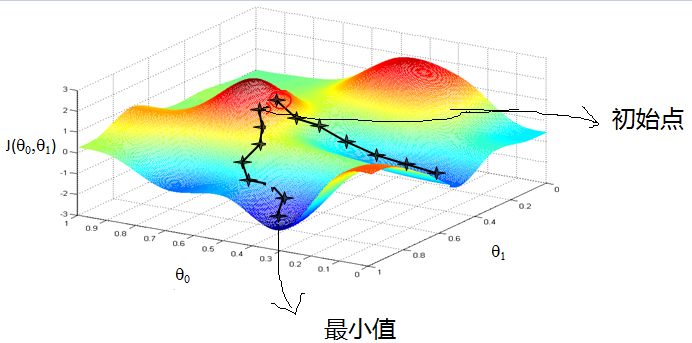
  1. 先确定向下一步的步幅大小，称之为Learning rate;
  2. 任意给定一个初始值：$\theta_0,\theta_1,…,\theta_n$;
  3. 确定一个向下的方向，并向下走预先规定的步伐，并更新$\theta_0,\theta_1,…,\theta_n$;
  4. 当下降的高度小于某个定义的阈值时，停止下降更新。

这就好比是下山，下一步的方向选的是最陡的方向。梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。θ 的更新方程如下：
$$
\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta)
$$
其中，偏导是：
$$
\frac{\partial}{\partial\theta_j}J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})x_j^{(i)}
$$

代码实例

本部分我们将采用2种方式实现逻辑回归模型，一种自己编写函数方法，一种调用sklearn中的方法库（LogisticRegression）。

自己实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import numpy as np
import random
import matplotlib.pyplot as plt
#sigmod函数，将值量化到0-1
def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))

# 梯度下降算法
def gradientDescent(x, y, theta, alpha, m, numIteration):
    '''
    :param x: 输入实例
    :param y: 分类标签
    :param theta: 学习的参数
    :param alpha: 学习率
    :param m: 实例个数
    :param numIteration: 迭代次数
    :return: 学习擦参数theta
    '''
    xTrans = x.transpose()  # 矩阵的转置
    J = [] # 存储损失的列表，方便绘图
    for i in range(0, numIteration):
        hypothsis = sigmoid(np.dot(x, theta)) #量化到0-1
        loss = hypothsis - y #计算误差
        cost = np.sum(loss ** 2) / (2 * m) #计算损失
        J.append(cost) # 将损失存入列表
        print("Iteration %d / Cost:%f" % (i, cost))
        gradient = np.dot(xTrans, loss) / m
        theta = theta - alpha * gradient  # 更新梯度
    plt.plot(J) # 可视化损失变化
    plt.show()
    return theta



# 创建数据，用作测试
def genData(numPoints, bais, variance):
    '''
       :param numPoints: 输入实例数目
       :param bais: 偏向
       :param variance: 方差
       :return 创建的数据 x,y
       '''
    # 实例（行数）、偏向、方差
    x = np.zeros(shape=(numPoints, 2))  # 初始化numPoints行2列(x1,x2)的全零元素矩阵
    y = np.zeros(shape=numPoints)  # 归类标签
    y_list = [0,1] # 标签列表y的取值
    for i in range(0, numPoints):
        x[i][0] = random.uniform(0, 1) * variance # 创建X的特征对
        x[i][1] = (i + bais) + random.uniform(0, 1) * variance
        random.shuffle(y_list) # 给X特征对附上随机的0 1 标签
        y[i] =y_list[0]
    return x, y

x, y = genData(100, 2, 5)
#print(x)
#print(y)

#x和y的维度
m, n = np.shape(x)
n_y = np.shape(y)

numIteration = 100000
alpha = 0.0005
theta = np.ones(n)  # 初始化theta
theta = gradientDescent(x, y, theta, alpha, m, numIteration)
print(theta) #output [-0.14718538  0.00381781]

Sklearn实现

1
2
3
4
5
6
from sklearn.linear_model import LogisticRegression
# 调用sklearn自带的逻辑回归方法
sk = LogisticRegression(max_iter=100000)
sk.fit(x, y) # 此处的x和y与上面自己实现的一致
print(sk.intercept_)
print(sk.coef_) #output [-0.11612453  0.00272452]

我们发现自己闪现求解的$\theta$值与sklearn中的相比，还是存在一定误差的，这是因为sklearn中的方法 LogisticRegression有很多参数进行了详细的优化，详情参见https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn-linear-model-logisticregression

Cost损失可视化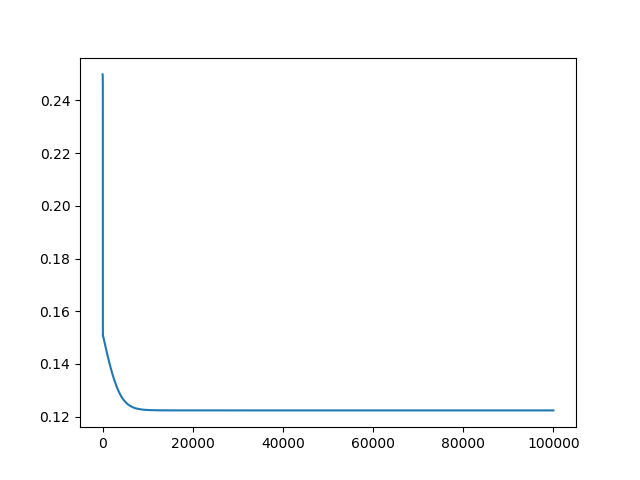

模型优缺点

优点：

  1. 适合需要得到一个分类概率的场景
  2. 计算代价不高，容易理解实现。LR在时间和内存需求上相当高效
  3. LR对于数据中小噪声的鲁棒性很好

缺点：

  1. 容易欠拟合，分类精度不高
  2. 对异常值敏感
------ 本文结束------
bluesliuf wechat
坚持技术分享，欢迎大家扫码交流！