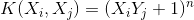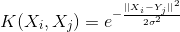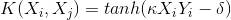机器学习方法之SVM

发表于 | 更新于 | 分类于 | 阅读次数
字数统计 4k | 阅读时长 16

支持向量机（support vector machine）,简称SVM，最早在1963年，由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 提出。目前的版本(soft margin)是由Corinna Cortes 和 Vapnik在1993年提出，并在1995年发表。

背景

深度学习（2012）出现之前，SVM被认为机器学习中近十几年来最成功，表现最好的算法。SVM本质上是一种二分类器，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。
看下图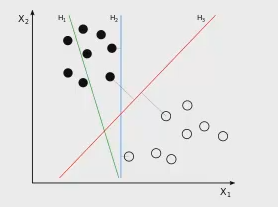

在这个二维的平面中，用一条直线将上面的点分成两类，显然 H1 无法将点区分开，而H2 和 H3 都可以，但这两条哪个更好呢？作为分界线，H3 是更合适的，因为分界线其两边有尽可能大的间隙，这样的好处之一就是增强分类模型的泛化能力，能较为正确的分类预测新的实例。

上面的例子是在二维平面，我们找的是一条直线。假如在三维空间，我们要找的就是一个平面。总的来说就是要寻找区分两类的超平面(hyper plane )，使边界(margin )最大。在一个 n 维空间中，超平面的方程定义为:

               $a_1x_1+a_2x_2+…+a_nx_n = b$

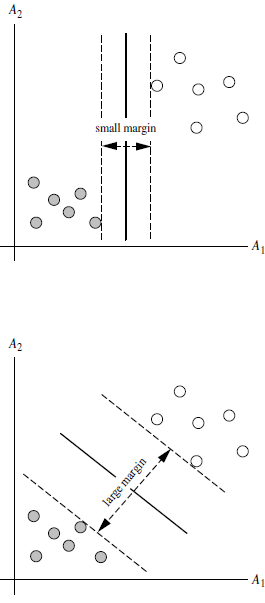
总共可以有多少个可能的超平面？无数条。我们要寻找的超平面是到边界一测最近点的距离等于到另一侧最近点的距离，在这个边界中，边界两侧的超平面平行。

点到超平面的距离

在二维平面中，计算点 (x0, y0) 到线ax + by + c = 0的距离是: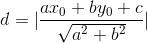

在 n 维空间中，点到超平面的距离：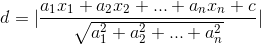

将点的坐标和系数都向量化表示，距离公式可以视为: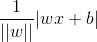

其中 w = {w0, w1, w2,...,wn}
我们寻找超平面时，先寻找各分类到超平面的距离最小，再寻找距离之和最大的超平面。共N 个训练点，点的坐标记为xi，结果分类为yi，构成 (xi, yi)：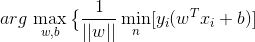

常见的SVM是 二分类模型，因此一般yi 有两种取值为 1 和 -1，取这两个值可以简化求解过程。

超平面推导

在 (xi, yi) 中，我们用 xi 表示了点的坐标，yi 表示了分类结果。超平面表示如下：
$$
w^Tx + b = 0
$$
在超平面的上方的点满足：
$$
w^T + b > 0
$$
在超平面的下方的点满足：
$$
w^T + b < 0
$$
因为 yi 只有两种取值 1 和 -1。因此就满足：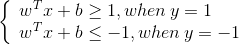

整合这两个等式（左右都乘以 yi，当yi是负值时，不等号要改方向）得：
$$
y_i(w^T + b)\geq1,\forall{i}
$$

支持向量

所有坐落在边界的边缘上的点被称作是 “支持向量”。分界边缘上的任意一点到超平面的距离为:$\left|\frac{1}{w}\right|$。
其中，||w|| 是向量的范数(norm)，或者说是向量的模。它的计算方式为：
$$
\left|{w}\right| = \sqrt{w * w} = \sqrt{w_1^2 + w_2^2 +…+ w_n^2}
$$
所以最大边界距离为$\left|\frac{2}{w}\right|$。

找出最大边界的超平面

  1. 利用一些数学推导，把 yi(w^T*x + b) >= 1 变为有限制的凸优化问题( convex quadratic optimization )；

  2. 利用Karush-Kuhn-Tucker( KKT ) 条件和拉格朗日公式，可以推出 MMH 可以被表示为以下的“决定边界( decision boundary)”

$$
d(X^T) = \sum_{i=1}^{l}y_ia_iX_iX^T + b_0
$$

上述公式中各个符号含义如下：

  • l：表示 支持向量点 的个数；
  • yi : 第i个支持向量点；
  • Xi ：支持向量的类别标记( class label )；
  • ai 与b0：都是单一数值型参数。

对于测试实例，代入以上公式，按得出结果的正负号来进行分类。

SVM 算法有下面几个特性：

  1. 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以 SVM 不太容易产生过拟合(overfitting )的情况；
  2. SVM 训练出来的模型完全依赖于支持向量，即使训练集里所有非支持向量的点都被去除，重新训练，结果仍然会得到完全一样的模型；
  3. 一个 SVM 如果训练得出的支持向量个数比较小，那训练出的模型比较容易被泛化

线性不可分

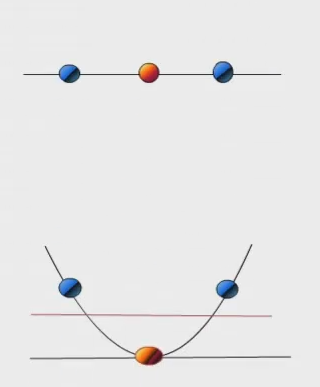
在有些情况下，我们无法用一条直线对实例进行划分。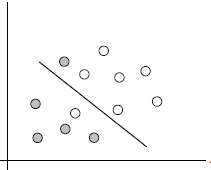

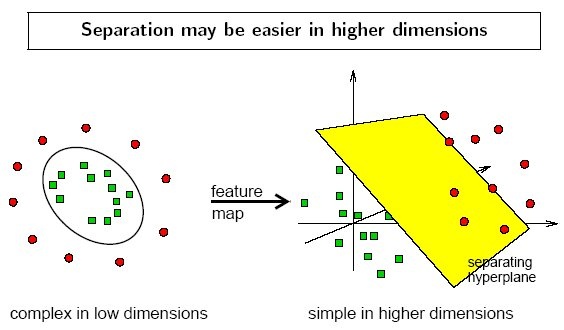
其实在很多情况下，数据集在空间中对应的向量不可被一个超平面区分开。这种时候我们要采取以下2个步骤：

  1. 利用一个非线性的映射把原数据集中的向量点转化到一个更高维度的空间中；
  2. 在这个高维度的空间中找一个线性的超平面来进行可区分处理。

    如上图表示的，将其从一维转为二维空间，然后在二维空间进行求解。动态演示

高纬空间（核方法）

我们如何将原始数据转化到高纬空间呢，举个例子，在三维空间中的向量 X = (x1, x2, x3)转化到六维空间 Z 中去，令: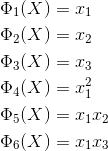

新的决策超平面为: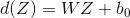

其中，W和Z 都是向量，这个超平面是线性的，解出 W 和b 后，带回原方程：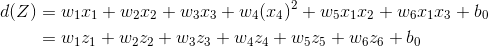

上面转换的求解过程中，需要计算内积，而内积的复杂度非常高，这就需要使用到核方法。

核方法
在处理非线性的情况中，SVM 选择一个核函数 ( kernel trick )，通过函数 k(.,.) 将数据映射到高维空间。支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维空间中构造出最优分离超平面。
核函数例子： 假设两个向量：x = (a1, a2, a3) y = (b1, b2, b3) ，定义方程：

1
f(x) = (x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3)

假设核函数为:K(x, y) = (<x, y>)^2 , 且设x = (1, 2, 3) y=(4, 5, 6) 则有：

1
2
3
f(x) = (1, 2, 3, 2, 4, 6, 3, 6, 9)
f(y) = (16, 20, 24, 20, 25, 36, 24, 30, 36)
<f(x), f(y)> = 16 + 40 + 72 + 40 + 100 + 180 + 72 + 180 + 324 = 1024

核函数计算为: K(x, y) = (4 + 10 + 18 ) ^2 = 32^2 = 1024 ，相同的结果，使用核函数计算会快很多。

核函数能很好的避开直接在高维空间中进行计算，而结果却是等价的。
常见的几个核函数 (kernel functions)有

  1. h度多项式核函数(polynomial kernel of degree h)
  2. 高斯径向基核函数(Gaussian radial basis function kernel)
  3. S型核函数(Sigmoid function kernel)

    如何选择使用哪个核函数？ 根据先验知识，比如图像分类，使用RBF，尝试不同的核函数，根据结果准确度而定。

多分类

SVM 常见的是二分类模型，如果空间中有多个分类，比方有猫，狗，鸟。那么SVM就需要对每个类别做一次模型，是猫还是不是猫？是狗还是不是狗？是鸟还是不是鸟？从中选出可能性最大的。也可以两两做一次SVM：是猫还是狗？是猫还是鸟？是狗还是鸟？最后三个分类器投票决定。因此，多分类情况有两种做法：

  1. 对于每个类，有一个当前类和其他类的二类分类器( one-versus-the-rest approach)
  2. 两两做一次二类分类器( one-versus-one approace )

代码实例

几个点的分类


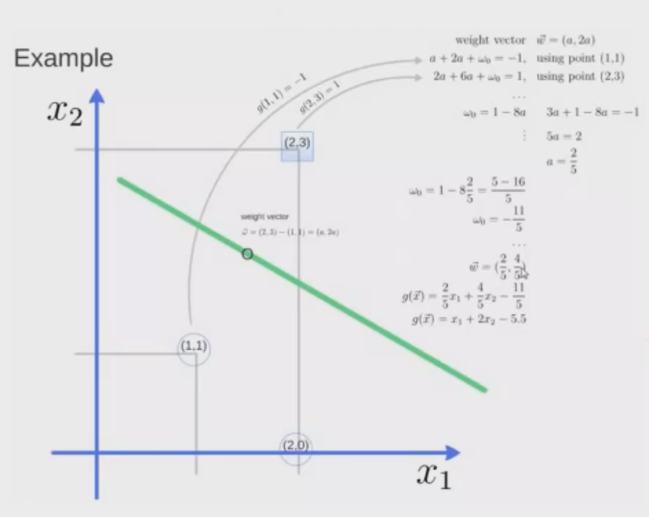
在上面的二维空间中，有三个点：(1, 1) (2, 0) (2, 3) 。前两个点属于一类，第三个点属于另一类，我们使用这个例子来简单说明 sklearn 中 SVM 的初步用法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn import svm

x = [[2,0],[1,1],[2,3]]
y = [0,0,1]
classify = svm.SVC(kernel='linear')
classify.fit(x,y)
print(classify)
#打印支持向量 output:[[1. 1.],[2. 3.]]
print(classify.support_vectors_)
#打印支持向量在数据实例中的索引 output:[1 2]
print(classify.support_)
#打印每一类中支持向量的个数 output:[1 1]
print(classify.n_support_)
#预测新的实例 output:[1]
print(classify.predict([[2,3]]))

上面的例子中有两个点是支持向量：(1, 1) (2, 3)，通过clf.support_vectors_可以得到具体的点。这些支持向量点在数据集中的索引可以通过 clf.support_ 得到。在这个例子中，分界线的两侧各有一个支持向量，可以通过clf.n_support_得到，结果为 [1, 1]。

多个点的分类

我们增加点的个数，并将超平面画出来，进行可视化展示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
from sklearn import svm
import pylab as pl

np.random.seed(0) #设置相同的seed,每次产生的随机数相同
'''
生成2个（20*2）的二维数组，然后按列将它们连接组成（40*2）的二维数组
生成的点服从正态分布，-[2,2],+[2,2]会让点靠左下方和右上方
'''
X = np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]]
Y = [0]*20 + [1]*20 #给这40个点分类，标记为0和1
#print(X.shape)
#print(Y)

classify = svm.SVC(kernel='linear') #构造SVM分类模型
classify.fit(X,Y)

'''
利用上面的40个点来画一个二维的分类平面图，
假设超平面方程为w0x + w1y + b = 0 转为点斜式就是: y = -(w0/w1)x - (b/w1) ：
调用classify，获取w的值
'''
w = classify.coef_[0]
a = -w[0]/w[1]
xx = np.linspace(-5,5) #在（-5，5）区间内生成一些连续值，方便作图
yy = a*xx - (classify.intercept_[0])/w[1]
#print(w)
#print(a)

'''
绘制经过支持向量，并与超平面平行的上下2条直线
由于平行，因此斜率相同，只是截距不同
'''
b = classify.support_vectors_[0] #第一分类中的第一个支持向量点
yy_down = a*xx + (b[1]-a*b[0])
b = classify.support_vectors_[-1] #第二分类中的最后一个支持向量点
yy_up = a*xx + (b[1]-a*b[0])
#print(classify.support_vectors_)

'''
将所有的点、超平面和2条分界线绘制出来
k-为实线，即超平面线
k--为虚线，2条边界线
'''
pl.plot(xx, yy, 'k-')
pl.plot(xx, yy_down, 'k--')
pl.plot(xx, yy_up, 'k--')
#单独标记出支持向量点
pl.scatter(classify.support_vectors_[:, 0], classify.support_vectors_[:, 1], s=80, facecolors='none')
pl.scatter(X[:, 0], X[:, 1], c=Y,cmap=pl.cm.Paired )
pl.axis('tight')
pl.show()

可视化结果如下：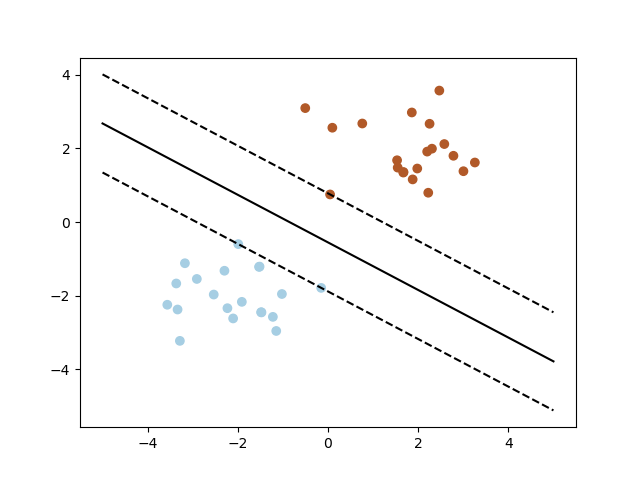

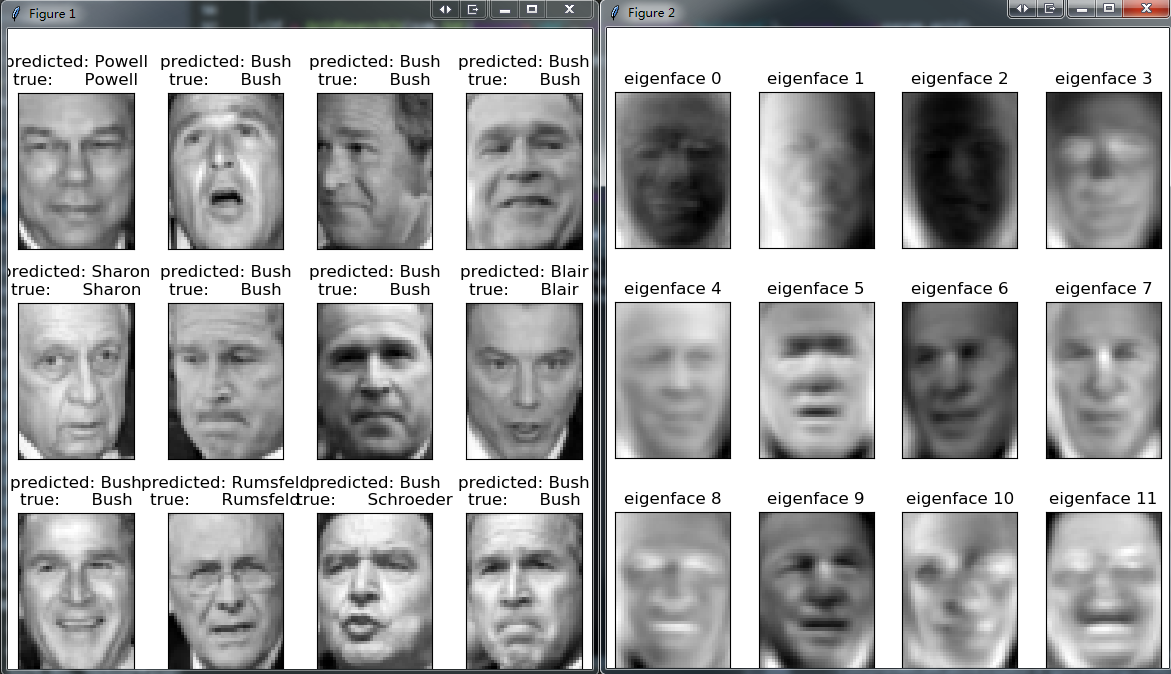
SVM人脸分类

我们构建SVM模型分类人脸并进行可视化展示，数据集（lfw）默认存储在~/scikit_learn_data 文件夹中。代码讲解见注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
from __future__ import print_function

from time import time
import logging
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import GridSearchCV
from sklearn.decomposition import PCA
from sklearn.svm import SVC
from sklearn import metrics

#输出日志信息
logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s')
'''
下载数据集（国外名人）lfw，可以手动下载：https://ndownloader.figshare.com/files/5976015
min_faces_per_person表示提取每类人超过这一数目的数据集
#resize调整每张人脸图片的比例，默认是0.5
'''
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
n_samples, h, w = lfw_people.images.shape # 返回数据集的实例数及图片宽和高
X = lfw_people.data #获取每个实例的特征
n_features = X.shape[1] #获取每个实例的特征数
y = lfw_people.target #标签数据，及每个人的身份
target_names = lfw_people.target_names #存储每个人的人名
n_classes = target_names.shape[0] # 有几类人

print("===== 数据集中信息 =====")
print("数据个数(n_samples):", n_samples) # 1288
print("特征个数，维度(n_features):", n_features) # 1850
print("结果集类别个数(n_classes):", n_classes) # 7

'''
调用train_test_split方法拆分训练集合测试集
test_size=0.25表示随机抽取25%的测试集
'''
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.25)

'''
原始数据的特征向量维度非常高，意味着训练模型的复杂度非常高,我们要采用PCA降维，
保存的组件数目，也即保留下来的特征个数，此处我们选择150
'''
n_components = 150
print("Extracting the top %d eigenfaces from %d faces" % (n_components, X_train.shape[0]))
t0 = time()
pca = PCA(n_components=n_components,whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))

#降维后提取每个实例的特征点
eigenfaces = pca.components_.reshape((n_components,h,w))

print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
#把训练集和测试集特征向量转化为更低维的矩阵
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("done in %0.3fs" % (time() - t0))

#构建SVN分类模型
print("Fitting the classifier to the training set")
t0 = time()

'''
C是一个对错误部分的惩罚
gamma的参数对不同核函数有不同的表现，gamma表示使用多少比例的特征点
使用不同的c和不同值的gamma，进行多个量的尝试
此处组成5*6的网格参数点，然后进行搜索，最后选出准确率最高模型
'''
param_grid= {'C':[1e3, 5e3, 1e4, 5e4, 1e5],
             'gamma':[0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1]
             }
clf = GridSearchCV(SVC(kernel='rbf',class_weight='balanced'),param_grid)
clf = clf.fit(X_train_pca,y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)

#评估测试集
print("Predicting people's names on the test set")
t0 = time()
y_pred = clf.predict(X_test_pca)
print("done in %0.3fs" % (time() - t0))

'''
classification_report查看每一类的各种评价指标
confusion_matrix(混淆矩阵) 是建一个 n x n 的方格，横行和纵行分别表示真实的每一组测试集
的标记和测试集标记的差别，通常表示这些测试数据哪些对了，哪些错了。
这个对角线表示了哪些值对了，对角线数字越多，就表示准确率越高。
'''
print(metrics.classification_report(y_test,y_pred,target_names=target_names))
print(metrics.confusion_matrix(y_test, y_pred, labels=range(n_classes)))

#将测试结果可视化展示
def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
    plt.figure(figsize=(1.8 * n_col, 2.4 * n_row)) # 定义画布的大小
    plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35) # 调整图片显示位置
    for i in range(n_row * n_col):
        plt.subplot(n_row, n_col, i + 1) #画布划分
        plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray) # 图片显示
        plt.title(titles[i], size=12) # 标题
        #获取或设置x、y轴的当前刻度位置和标签
        plt.xticks(())
        plt.yticks(())

#预测函数归类标签和实际归类标签打印
#返回预测人脸和测试人脸姓名的对比title
def title(y_pred, y_test, target_names, i):
    '''
    rsplit（' ',1）从右边开始以右边第一个空格为界，分成两个字符
    组成一个list
    此处代表把'姓'和'名'分开，然后把后面的姓提出来
   末尾加[-1]代表引用分割后的列表最后一个元素
    '''
    pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
    true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
    return 'predicted: %s\ntrue:      %s' % (pred_name, true_name)

#预测出的人名
prediction_titles = [title(y_pred, y_test, target_names, i)
                     for i in range(y_pred.shape[0])]

#测试集的特征向量矩阵和要预测的人名打印
plot_gallery(X_test, prediction_titles, h, w)
#打印原图和预测的信息
eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]
#调用plot_gallery函数打印出实际是谁，预测的谁，以及提取过特征的脸
plot_gallery(eigenfaces, eigenface_titles, h, w)

plt.show()

程序运行结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
===== 数据集中信息 =====
数据个数(n_samples): 1288
特征个数，维度(n_features): 1850
结果集类别个数(n_classes): 7
Extracting the top 150 eigenfaces from 966 faces
done in 0.309s
Projecting the input data on the eigenfaces orthonormal basis
done in 0.025s
Fitting the classifier to the training set
done in 23.043s
Best estimator found by grid search:
SVC(C=1000.0, cache_size=200, class_weight='balanced', coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma=0.001, kernel='rbf',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)
Predicting people's names on the test set
done in 0.047s
                   precision    recall  f1-score   support

     Ariel Sharon       0.81      0.62      0.70        21
     Colin Powell       0.72      0.88      0.79        58
  Donald Rumsfeld       0.66      0.73      0.69        26
    George W Bush       0.88      0.86      0.87       130
Gerhard Schroeder       0.81      0.69      0.75        32
      Hugo Chavez       1.00      0.69      0.82        13
       Tony Blair       0.81      0.83      0.82        42

        micro avg       0.81      0.81      0.81       322
        macro avg       0.81      0.76      0.78       322
     weighted avg       0.82      0.81      0.81       322

[[ 13   4   2   2   0   0   0]
 [  0  51   1   3   1   0   2]
 [  1   2  19   3   0   0   1]
 [  1  10   5 112   2   0   0]
 [  0   1   1   5  22   0   3]
 [  1   1   0   0   0   9   2]
 [  0   2   1   2   2   0  35]]

可视化结果展示如下

参考资料
机器学习-支持向量机的SVM
fetch_lfw_people安装失败

------ 本文结束------
bluesliuf wechat
坚持技术分享，欢迎大家扫码交流！